概要
今回は、pythonで単回帰分析(OLS: 最小二乗法)を行ってみました。未来予測より、2変数間の関係を分析することに着目してみます。使用するライブラリですが、回帰はsklearnにもありますが、今回の着目点(2変数の関係を分析)ではstatsmodelsが便利なので、そちらを使っていきます。
また、lmdiagというライブラリを使ってみます。こちらは、statsmodelsで作ったモデルを入力として回帰診断(可視化)ができるものです。
実装
1.データ作成
正の相関がある2変量正規分布より乱数生成して作成します。
# ライブラリ
import numpy as np
from numpy.random import multivariate_normal
from scipy import stats
import statsmodels.api as sm
import lmdiag
import matplotlib.pyplot as plt
from IPython.display import display
# データ作成
base_mu = [10, 50]
base_sigma = [[20, 10], [10, 20]]
data = multivariate_normal(base_mu, base_sigma, 500)
print(f"data shape: {data.shape}")
# 相関, p値(無相関の検定)
corr = stats.pearsonr(data[:,0], data[:, 1])
print(f"corr: {corr.statistic:.3}, p: {corr.pvalue}")
# 散布図
plt.rcParams["figure.figsize"] = (4, 3)
plt.scatter(data[:,0], data[:, 1])
plt.title("scatter")
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.show()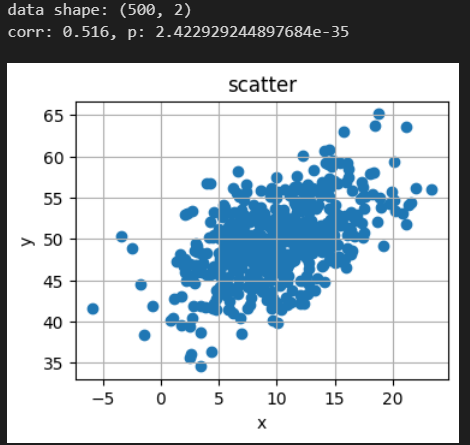
2.単回帰 実施
# 単回帰分析
# X (切片列含める) , y
X = sm.add_constant(data[:, [0]])
y = data[:, 1]
print(f"X shape: {X.shape}")
print(f"y shape: {y.shape}")
# 回帰実施
model = sm.OLS(y, X).fit()
result = model.summary()
# 予測値, 標準化残差(内部スチューデント化残差)
fittedvalues = model.fittedvalues
e = model.get_influence().resid_studentized_internal
print(f"fittedvalues shape: {fittedvalues.shape}")
print(f"e shape: {e.shape}")
# サマリ
display(result)
# 予測値のプロット(赤線)
plt.scatter(data[:,0], data[:, 1])
plt.plot(data[:,0], fittedvalues, color="red", label="fittedvalues")
plt.title("scatter, fittedvalues")
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.show()
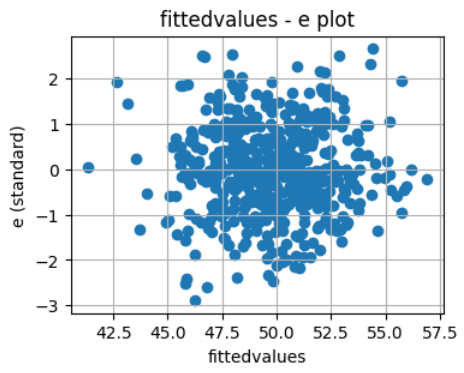
# 残差プロット (x: 予測値, y: 標準化残差)
plt.scatter(fittedvalues, e)
plt.title("fittedvalues - e plot")
plt.xlabel("fittedvalues")
plt.ylabel("e (standard)")
plt.grid()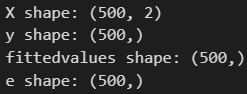
3.lmdiagで回帰診断
使い方は簡単です。下記の通り、statsmodelsで作ったモデルオブジェクトを入力として、lmdiagの関数を呼び出すだけでグラフが表示されます。
# lmdiagで回帰診断
plt.figure(figsize=(7, 7))
lmdiag.plot(model)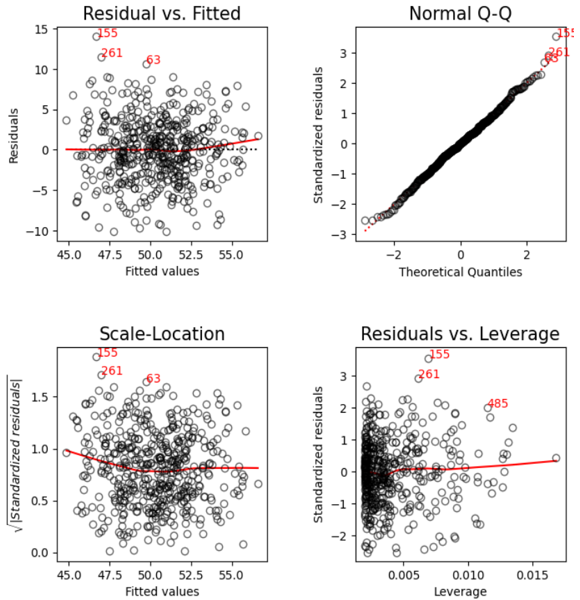
左下: ②Scale-Location
右上: ③Nomal Q-Q
右下: ④Residuals vs. Leverage
4.上記2、3の結果の整理・考察
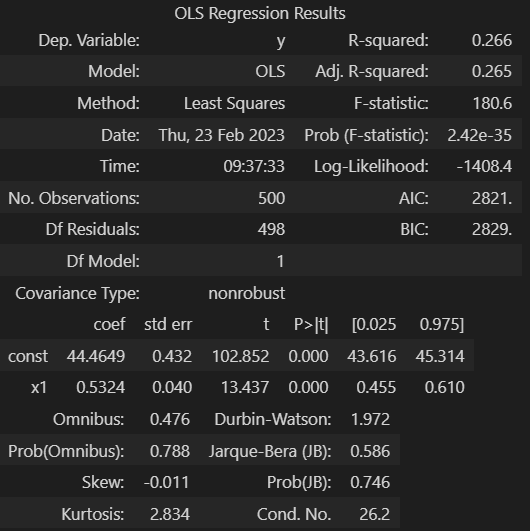
- 「2.①結果サマリ」について
- R-squared: 0.266 / Adj. R-squared: 0.265
- 上記は「決定係数」、「自由度調整済み決定係数」
- 値が1に近ければモデルの当てはまりが良い(残差が小さい)
- 結果は 0.265 あたりなので、当てはまりがあまり良くはなさそう。
- ただ、グラフ②を見る感じ、そんな悪いようには見えないので、外れ値の影響で上記数値なのかもしれない。外れ値除外で改善できるかもしれない。
- Prob (F-statistic): 2.42e-35
- 上記は「F検定の統計量のp値」、ここでいう検定は(ざっくり言うと)「モデル式は成り立つといえるか?」であり、詳細としては「帰無仮説を “切片含む回帰係数全てが 0 “としたときの検定」です。
- 本数値は 0 に大変近いので、帰無仮説(上記)は棄却できると考えます。つまりは、「本モデル式は成り立つ」と考えます。
- const, x1 の coef , P>|t|
- const の行は「切片」、x1 の行は 「説明変数の回帰係数」についてです。coef はそれらの「値」、P>|t| は「それぞれについてのt検定の統計量のp値」です。ここでいう検定は「帰無仮説を “対象値(切片, 回帰係数) が 0 ” としたときの検定」であり、ざっくり言うと、切片や説明変数それぞれについて「モデルに必要なものか?」を調べる検定です。
- それぞれのp値は(ほぼ)0なので、切片や説明変数はモデルに必要なものと考えます。
- Prob(Omnibus): 0.788, Prob(JB): 0.746
- 上記は「オムニバス検定、ジェルクベラ検定の統計量のp値」です。両検定は「モデルにおける誤差項の正規性」を調べるものであり、帰無仮説は「誤差項は正規分布」です。
- 誤差項が正規分布であることは、「切片や回帰係数がMVUE (最小分散不偏推定量) 、つまり “目的変数から作成できる不偏推定量(期待値が真値と一致)の中で最も分散が小さい(ざっくり言うと精度高い)” 」であるための条件の一つです。
- 今回のp値は大きいため、帰無仮説は棄却できない、つまりは、「正規分布でないとは言い切れない」と考えます。
- Durbin-Watson: 2.104
- 上記は「ダービンワトソン統計量の値」であり、「誤差項の自己相関(1階)があるか?」を調べるものです。自己相関が無い事は、上記のBLUEやMVUEの前提条件の一つです。
- 帰無仮説は「自己相関ρ = 0」であり、「2(1-ρ)」を推定値になっています。つまりは、「値が2に近ければ無相関(を否定できない)、0に近ければ正の相関、4に近ければ負の相関がある」と考えます。
- 今回の結果は2に近いので、「無相関(を否定できない)」と考えます。
- R-squared: 0.266 / Adj. R-squared: 0.265
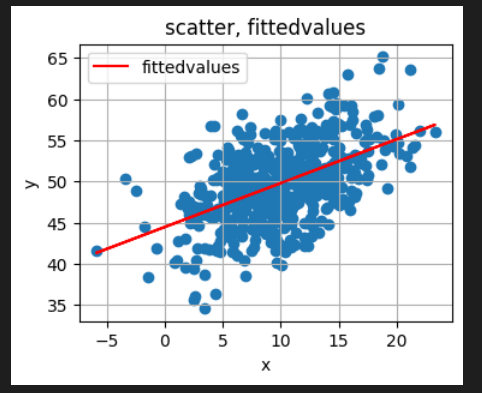
- 「2.③残差プロット」について
- 上記はx軸に「モデル式から得られた目的変数の予測値」、y軸に「標準化した残差(正確には “内部スチューデント化残差” )」とした散布図です。
- 本図で知りたいことは、「(任意の説明変数の値に対して)誤差項の分散が一定であるか?」です。分散が一定であることは、「切片や回帰係数がBLUE (最良線形不偏推定量) 、つまり “目的変数の線形関数で作成できる不偏推定量の中で最も分散が小さい“」であるための条件の一つです。(BLUEと、上記にあるMVUEとの違いは「対象とする範囲の違い」であり、「前者は線形関数の範囲に限っている」形です。)
- 本図で、「x軸のどこでもy軸においてプロットのバラつきは同じくらい」であれば誤差項の分散が一定であると考えます。
- 今回の図では、(x軸それぞれについて、データ量の大小に結構差があるので判断が難しく感じますが、)「断言はできないが、強いて言うならバラつきは同じように見える」と感じます。
- 「3.①~④」について
- ①Residual vs. Fitted / ②Scale-Location
- 上記2つのグラフは(大枠として)残差プロットです。
- x軸は予測値(共通)であり、y軸については、①は「残差」、②は「標準化残差の絶対値の平方根」です。
- 着眼点は上記「2.③残差プロット」の件と同様です。
- ③Nomal Q-Q
- 上記は「残差のQ-Qプロット」です。(Q-Qプロットについては別記事をご参照ください)
- 残差は「誤差項の推定値」なので、「誤差項が正規分布になっているか?」を調べるものです。上述したように「誤差項が正規分布」は「MVUE」の条件の一つです。
- 散布図の各点が、赤の点線に合う形であれば正規分布と考えます。今回の結果は赤の点線に合う形なので、正規分布と考えます。
- ④Residuals vs. Leverage
- 上記は、y軸を「標準化残差」、x軸を「レバレッジ」とした散布図です。「L-Rプロット」とも呼びます。
- レバレッジとは、「(説明変数から作成される)ハット行列の対角成分」(データ数分の成分が存在)であり、(説明変数について)「各データの “全体平均からの離れ度合い”」を示す値です。
- つまり、本図は「目的変数、説明変数の外れ値の存在、影響」を調べるものです。
- 例えば「レバレッジが大きいけど、残差が小さい」ような点があったら、「外れ値に、モデルが合わせにいこうとし過ぎてる」可能性があるかもしれません。その可能性がある場合は対象データを除いてモデルを作った方が汎化性が高いかもしれません。
- ①Residual vs. Fitted / ②Scale-Location
補足
上記の「結果の整理・考察」において詳細を学びたい方は下記記事の書籍が参考になります。