【python】ロジスティック回帰分析

statsmodelsを用いて、ロジスティック回帰モデルを作り、当てはまり度合いを見てみたいと思います。

１．実装

1-1. データ作成

今回はタイタニックのデータを使ってみたいと思います。簡単に、数値変数のみを説明変数にしてみます。

# ライブラリ
import seaborn as sns
import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix, classification_report, roc_curve, roc_auc_score

import matplotlib.pyplot as plt
from IPython.display import display

# data
data = sns.load_dataset('titanic')
data = data[data.describe().columns]
data = data.fillna(data.mean())
print(data.survived.value_counts())
display(data.head())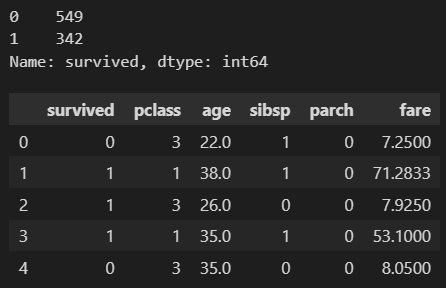

1-2. ロジスティック回帰の実施

数値の大きさが異なるので、各説明変数は標準化の上、モデリングします。ロジスティック回帰を行うために、sm.GLMのfamilyパラメータを「sm.families.Binomial()」とします。
※本記事では、後続の1-3でなく、こちらの結果をメインに後続で確認していきます。

# ロジスティック回帰

target = "survived"
features = ["pclass", "age", "sibsp", "parch", "fare"]
y = data[target].to_numpy()
X = StandardScaler().fit_transform(data[features])
print(f"y shape: {y.shape}")
print(f"X shape: {X.shape}")

model = sm.GLM(y, X, family=sm.families.Binomial()).fit()
model.summary()

1-3. 予測値と正解を比較

※参考までに記載していますが、後続の結果確認では上記1-2をメインに記載します。

# 予測と正解を比較

pred = np.array([(1 if val>=0.5 else 0) for val in model.fittedvalues])
metrics = classification_report(y, pred, output_dict=True)
print(f"acc: {metrics['accuracy']:.2%}")
for key, val in metrics['1'].items():
    if key != "support":
        print(f"{key}: {val:.2%}")
auc = roc_auc_score(y, model.fittedvalues)
print(f"auc: {auc:.2}")
# 混合行列
matrix = confusion_matrix(y, pred)
plt.figure(figsize=(4, 3))
sns.heatmap(matrix)
plt.show()
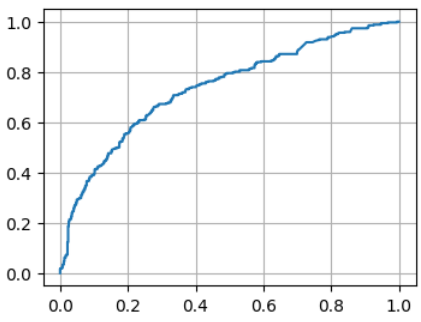
# ROC
roc_tup = roc_curve(y, model.fittedvalues)
plt.figure(figsize=(4, 3))
plt.plot(roc_tup[0], roc_tup[1])
plt.grid()
plt.show()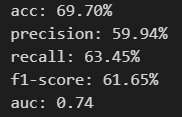

２．結果の確認

• 1-2.の結果(★サマリ)について
  1. Model Family: Binomial
     1. 上記は（仮定している）目的変数yの分布です。
     2. 今回はロジスティック回帰を実施しているため、「二項分布」となっています。
  2. Link Function: Logit
     1. 上記は（仮定している）リンク関数（連結関数）です。
     2. 今回はロジスティック回帰を実施しているため、「ロジット関数」（対数オッズ）となっています。
     3. 尚、リンク関数とは「目的変数の期待値を入力として、返す値を”説明変数の線形関数”と見なすもの」です。
  3. Df Residuals: 886
     1. 上記は「残差の自由度」です。
     2. Df は「自由度」の略称です。
  4. Log-Likelihood: -540.95
     1. 上記は「得られたモデルの対数尤度」です。対数であり尤度は0~1なので、非正の値をとり、0に近いほど尤度的に当てはまりが良いと考えます。
  5. Deviance: 1081.9
     1. 上記は「尤離度」であり、「(yの期待値の)予測値から得る尤度」と「前者の予測値を、yそのものにした尤度(フルモデルの尤度)」の比を対数化したものです。（ =2log{ [後者] / [前者] } ）
     2. なので、値は非負であり、0に近ければ、尤度的に当てはまりが良いと考えます。
     3. 今回は当てはまりが良いと言い難い感じだと思います。
  6. Pearson chi2: 974
     1. 上記は「ピアソン残差の平方和」であり、自由度は「残差の自由度」（Df Residuals: 886）のカイ二乗分布に（漸近的に）従います。
     2. 帰無仮説が「過分散でない」としたカイ二乗検定における統計量です。過分散とは、作ったモデルでは表現できないほどの大きなバラつきが有ることを意味します。
     3. 今回の結果では、p値が 2% 程なので、過分散、つまりは今回のモデルでは表現しきれないと考えるのが妥当そうです。
  7. Pseudo R-squ. (CS): 0.1109
     1. 上記は（Cox and Snellの）疑似決定係数です。「回帰係数を0とした時の尤度」との比を用いて決定係数を疑似的に表現する指標です。
     2. 注意点として、「上限が1になるとは限らない（より小さい可能性）」という点があります。
  8. x1～x5 の P>|z|
     1. 上記は各説明変数について、帰無仮説を「回帰係数=0」とした時のZ検定です。つまり、帰無仮説が棄却できるとき、「対象の説明変数は目的変数に対して意味をもつ」と考えます。
     2. 今回の結果はどれも10%有意である形である中、x4については5%有意でない形です。なので、他の説明変数に比べてx4（parch）は重要度合いが低い可能性があると思います。

３．補足

一般化線形モデルの詳細については、下記記事の書籍が参考になります。