概要
有名な距離として、マハラノビスの距離という、変数間の相関を踏まえた(中心からの)距離があります。(その距離自体の詳細は割愛しますが、)その距離を用いて外れ値を除外する実装例を記載します。
実装例
1.データ準備
2変量のデータを作成します。numpyを用いて、正の相関がある2変量正規分布より乱数生成します。
# 本記事で使うライブラリ
import numpy as np
from numpy.random import multivariate_normal
from scipy import stats
from scipy.spatial import distance
import matplotlib.pyplot as plt
# 乱数生成
base_mu = [10, 50]
base_sigma = [[200, 30], [30, 100]]
data = multivariate_normal(base_mu, base_sigma, 500)
print(f"data shape: {data.shape}")
fig, axes = plt.subplots(1, 3, figsize=(20,5))
axes = axes.ravel()
# 相関, p値(無相関の検定)
corr = stats.pearsonr(data[:,0], data[:, 1])
print(f"corr: {corr.statistic:.3}, p: {corr.pvalue}")
# 散布図
axes[0].scatter(data[:,0], data[:, 1])
axes[0].set_title("scatter")
axes[0].set_xlabel("x")
axes[0].set_ylabel("y")
axes[0].grid()
# 各列のヒストグラム
axes[1].hist(data[:,0], bins=50)
axes[1].set_xlabel("x")
axes[1].set_title("hist: x")
axes[1].grid()
axes[2].hist(data[:,1], bins=50)
axes[2].set_xlabel("y")
axes[2].set_title("hist: y")
axes[2].grid()
plt.show()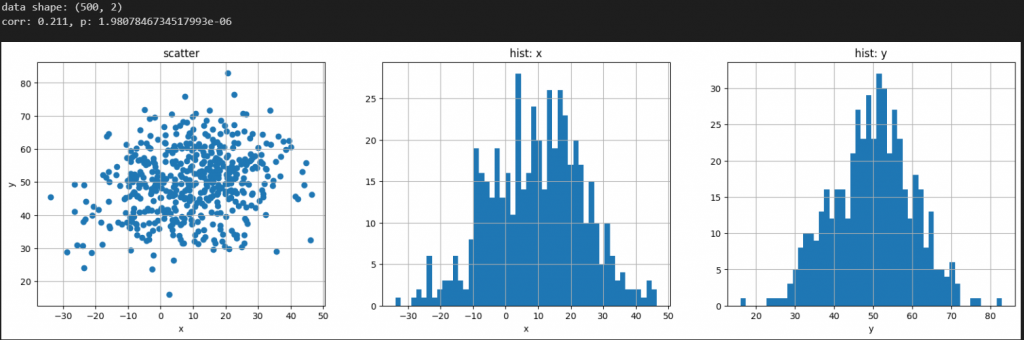
2.マハラノビスの距離を算出
作成したデータに対して、マハラノビスの距離を算出します。
# マハラノビスの距離を算出
# 距離算出
mean = data.mean(axis=0)
sigma = np.cov(data.T)
sigma_inv = np.linalg.inv(sigma)
print(f"mean: {mean}")
print(f"sigma_inv: {sigma_inv}")
dist = np.array(
[
distance.mahalanobis([x, y], mean, sigma_inv)
for x, y in data
]
)
print(f"dist shape: {dist.shape}")
# 距離のヒストグラム
plt.hist(dist, bins=50)
plt.title("hist: distance of mahalanobis")
plt.grid()
plt.show()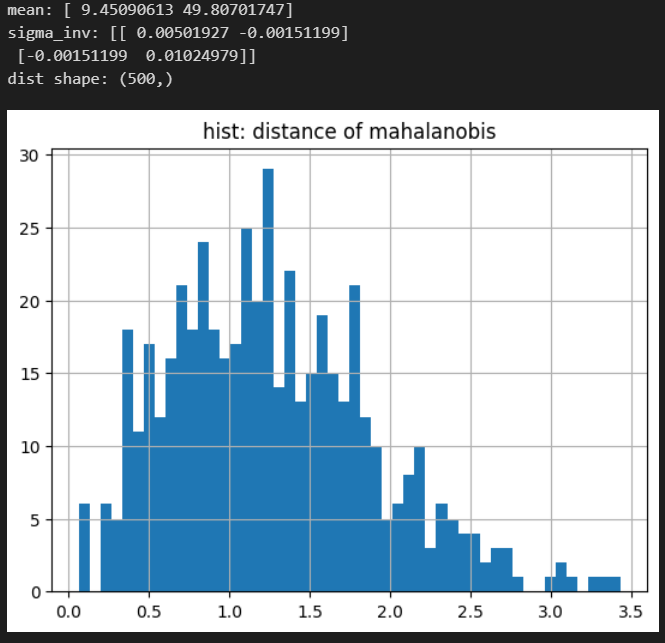
3.一定の距離を越えたものを外れ値として除外する
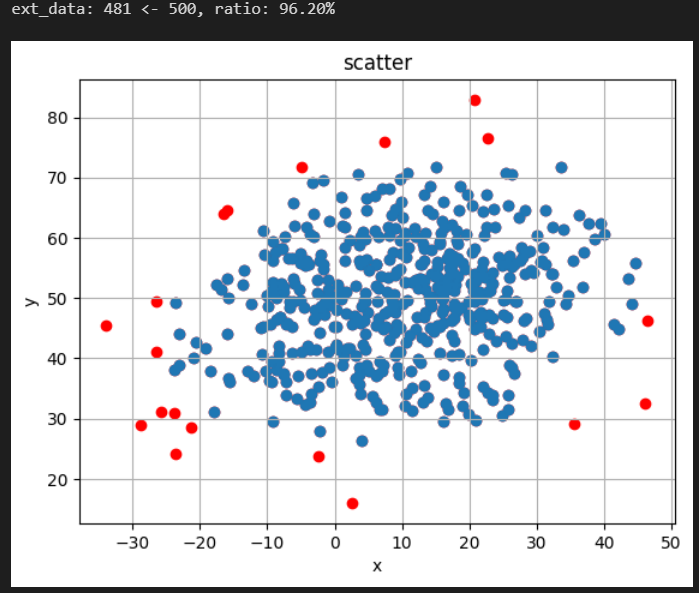
上記2.のヒストグラムより、2.5以上を外れ値と見なしてみたいと思います。「その外れ値はどの点にあたるか?」を散布図で確認してみます。赤点が外れ値と見なされたものになります。
# 距離が 2.5 以上を外れ値と見なし、それらを赤点とした散布図を作成
max_dist = 2.5
ext_data = np.array(
[
data[i, :]
for i in range(len(data))
if dist[i] < max_dist
]
)
print(f"ext_data: {len(ext_data)} <- {len(data)}, ratio: {len(ext_data)/len(data):.2%}")
# 散布図
plt.scatter(data[:,0], data[:, 1], color="red")
plt.scatter(ext_data[:,0], ext_data[:, 1])
plt.title("scatter")
plt.xlabel("x")
plt.ylabel("y")
plt.grid()
plt.show()