主成分分析 with Titanic Data

概要

kaggleで初めによく利用されるタイタニックデータを用いて、主成分分析をしてみました。
但し、今回は、予測することを目的として行ったのではなく、単に統計分析手法を用いて、データの特徴などを観察することを目的として行いました。
なので、train/testデータをまとめて主成分分析した次第です。

前提

• 主成分分析とは？
  複数の軸(変数)で表現されるデータに対して、”データのバラつき度が高くなる軸”を見つける手法。
  予測の際は次元圧縮のため、既存データの分析の際は要約のために行われることが多い。
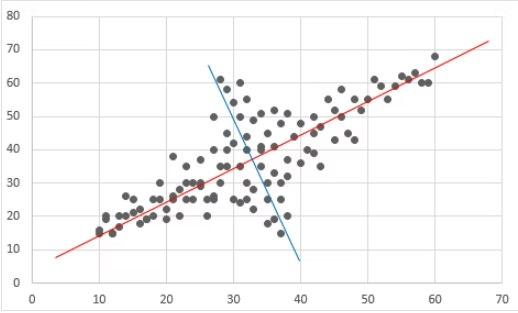
  下図(イメージ図)では、バラつきが最も高い赤軸、次に(赤軸に直交し)バラつきが高い青軸がある。
  このような赤軸、青軸を見つけるのが主成分分析である。

分析_概要

• 分析データ タイタニックデータ(train + test)。
  下記(kaggle)よりダウンロードできます。
  (但し、kaggleへのサインインが必要。)
  https://www.kaggle.com/c/titanic/data
• 確認ポイント
  〇 寄与率
  〇 固有ベクトル
  〇 因子負荷量
• 分析にて除外する変数
  今回は、簡易分析のため、前処理が難しい下記変数は除外して分析します。
  〇 Cabin
  〇 Ticket
  〇 Name

分析_詳細

１．ライブラリインポート

import os
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import display
from sklearn.decomposition import PCA

２．変数定義　(タイタニックデータcsv格納先など)

※フォルダ「data」にタイタニックデータcsv(train.csv , test.csv)を格納している前提のコード。

# カレントフォルダ
forlder_cur = os.getcwd()
print(" forlder_cur : {}".format(forlder_cur))
print(" isdir:{}".format(os.path.isdir(forlder_cur)))

# data格納先
folder_data = os.path.join(forlder_cur , "data")
print(" folder_data : {}".format(folder_data))
print(" isdir:{}".format(os.path.isdir(folder_data)))

# dataファイル

## train.csv
fpath_train = os.path.join(folder_data , "train.csv")
print(" fpath_train : {}".format(fpath_train))
print(" isdir:{}".format(os.path.isfile(fpath_train)))

## test.csv
fpath_test = os.path.join(folder_data , "test.csv")
print(" fpath_test : {}".format(fpath_test))
print(" isdir:{}".format(os.path.isfile(fpath_test)))

# id
id_col = "PassengerId"

# 目的変数
target_col = "Survived"

３．タイタニックデータ取り込み

下記コードで作成するデータ「all_data」(train + test)を後続で使用します。

# train.csv
train_data = pd.read_csv(fpath_train)
print("train_data :")
print("n = {}".format(len(train_data)))
display(train_data.head())

# test.csv
test_data = pd.read_csv(fpath_test)
print("test_data :")
print("n = {}".format(len(test_data)))
display(test_data.head())

# train_and_test
col_list = list(train_data.columns)
tmp_test = test_data.assign(Survived=None)
tmp_test = tmp_test[col_list].copy()
print("tmp_test :")
print("n = {}".format(len(tmp_test)))
display(tmp_test.head())

all_data = pd.concat([train_data , tmp_test] , axis=0)
print("all_data :")
print("n = {}".format(len(all_data)))
display(all_data.head())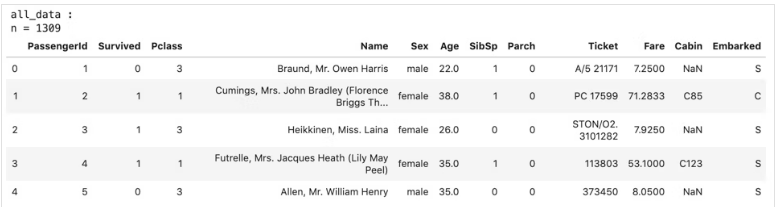

４．前処理

変数毎にダミー変数化や欠損補完、変数削除をして、作成するデータ「proc_all_data」を後続で使用します。

# コピー
proc_all_data = all_data.copy()

# Sex -------------------------------------------------------------------------
col = "Sex"

def app_sex(x):
    if x == "male":
        return 1
    elif x == 'female':
        return 0
    # 欠損
    else:
        return 0.5
proc_all_data[col] = proc_all_data[col].apply(app_sex)

print("columns:{}".format(col) , "-" * 40)
display(all_data[col].value_counts())
display(proc_all_data[col].value_counts())
print("n of missing :" , len(proc_all_data.query("{0} != {0}".format(col))))

# Age -------------------------------------------------------------------------
col = "Age"

medi = proc_all_data[col].median()
proc_all_data[col] = proc_all_data[col].fillna(medi)

print("columns:{}".format(col) , "-" * 40)
display(all_data[col].value_counts())
display(proc_all_data[col].value_counts())
print("n of missing :" , len(proc_all_data.query("{0} != {0}".format(col))))
print("median :" , medi)

# Fare -------------------------------------------------------------------------
col = "Fare"

medi = proc_all_data[col].median()
proc_all_data[col] = proc_all_data[col].fillna(medi)

print("columns:{}".format(col) , "-" * 40)
display(all_data[col].value_counts())
display(proc_all_data[col].value_counts())
print("n of missing :" , len(proc_all_data.query("{0} != {0}".format(col))))
print("median :" , medi)

# Embarked -------------------------------------------------------------------------
col = "Embarked"

proc_all_data = pd.get_dummies(proc_all_data , columns=[col])

print("columns:{}".format(col) , "-" * 40)
display(all_data.head())
display(proc_all_data.head())

# Cabin -------------------------------------------------------------------------
col = "Cabin"

proc_all_data = proc_all_data.drop(columns=[col])

print("columns:{}".format(col) , "-" * 40)
display(all_data.head())
display(proc_all_data.head())

# Ticket -------------------------------------------------------------------------
col = "Ticket"

proc_all_data = proc_all_data.drop(columns=[col])

print("columns:{}".format(col) , "-" * 40)
display(all_data.head())
display(proc_all_data.head())

# Name -------------------------------------------------------------------------
col = "Name"

proc_all_data = proc_all_data.drop(columns=[col])

print("columns:{}".format(col) , "-" * 40)
display(all_data.head())
display(proc_all_data.head())

proc_all_data :

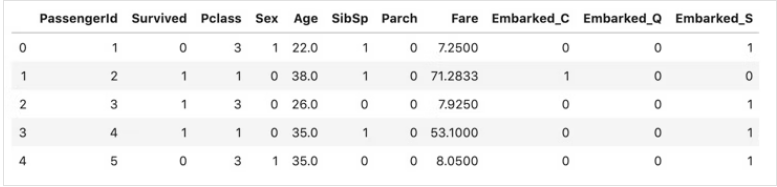
５．主成分分析 (寄与率 算出)

# 説明変数
feature_cols = list(set(proc_all_data.columns) - set([target_col]) - set([id_col]))
print("feature_cols :" , feature_cols)
print("len of feature_cols :" , len(feature_cols))

features = proc_all_data[feature_cols]

pca = PCA()
pca.fit(features)

print("主成分数 : " , pca.n_components_)
print("寄与率 : " , ["{:.2f}".format(ratio) for ratio in pca.explained_variance_ratio_])

下記結果の通り、第一主成分が圧倒的にバラつきが高い。
後続では第一主成分の固有ベクトル、因子負荷量を確認する。

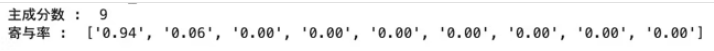
６．第一主成分の固有ベクトル

６-１．データ変形

# 固有ベクトル(第一主成分)

components_df = pd.DataFrame({
    "feature":feature_cols
    , "component":pca.components_[0]
})
components_df["abs_component"] = components_df["component"].abs()
components_df["rank_component"] = components_df["abs_component"].rank(ascending=False)

# ベクトル値の絶対値で降順ソート
components_df.sort_values(by="abs_component" , ascending=False , inplace=True)
display(components_df)

components_df :

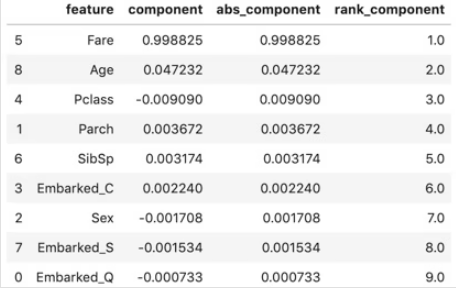
６-２．グラフ化

# グラフ作成
max_abs_component = max(components_df["abs_component"])
min_component = min(components_df["component"])
x_ticks_num = list(i for i in range(len(components_df)))

fig = plt.figure(figsize=(15,8))

plt.grid()
plt.title("Components of First Principal Component")
plt.xlabel("feature")
plt.ylabel("component")
plt.xticks(ticks=x_ticks_num , labels=components_df["feature"])

plt.bar(x_ticks_num , components_df["component"] , color="c" , label="components")
plt.plot(x_ticks_num , components_df["abs_component"] , color="r" , marker="o" , label="[abs] components")

plt.legend()

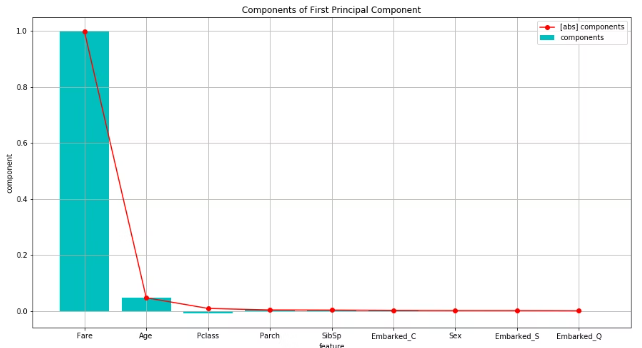
plt.show()

Fare(乗船料金)が圧倒的に大きく、その次はAge(年齢)。他はごく僅か。
固有ベクトルだけ見ると、Fareで要約された主成分であると見える。
しかし、固有ベクトルは対象変数の分散の大きさによって値が変わるため、後続で算出する因子負荷量を見て見る。

７．第一主成分の因子負荷量

７-１．データ変形

# 主成分得点(第一主成分)
score = pca.transform(features)[: , 0]

# 因子負荷量
dict_fact_load = dict()
for col in feature_cols:
    data = features[col]
    factor_loading = data.corr(pd.Series(score))
    dict_fact_load[col] = factor_loading

fact_load_df = pd.DataFrame({
    "feature":feature_cols
    , "factor_loading":[dict_fact_load[col] for col in feature_cols]
})
fact_load_df["abs_factor_loading"] = fact_load_df["factor_loading"].abs()
fact_load_df["rank_factor_loading"] = fact_load_df["abs_factor_loading"].rank(ascending=False)

# ベクトル値の絶対値で降順ソート
fact_load_df.sort_values(by="abs_factor_loading" , ascending=False , inplace=True)
display(fact_load_df)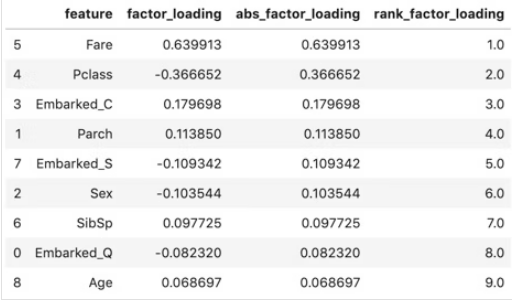

７-２．グラフ化

# グラフ作成
max_abs_factor_loading = max(fact_load_df["abs_factor_loading"])
min_factor_loading = min(fact_load_df["factor_loading"])
x_ticks_num = list(i for i in range(len(fact_load_df)))

plt.figure(figsize=(15,8))

plt.grid()
plt.title("Factor Lodings of First Principal Component")
plt.xlabel("feature")
plt.ylabel("factor loading")
plt.xticks(ticks=x_ticks_num , labels=fact_load_df["feature"])

plt.bar(x_ticks_num , fact_load_df["factor_loading"] , color="c" , label="factor loadings")
plt.plot(x_ticks_num , fact_load_df["abs_factor_loading"] , color="r" , marker="o" , label="[abs] factor loadings")

plt.legend()

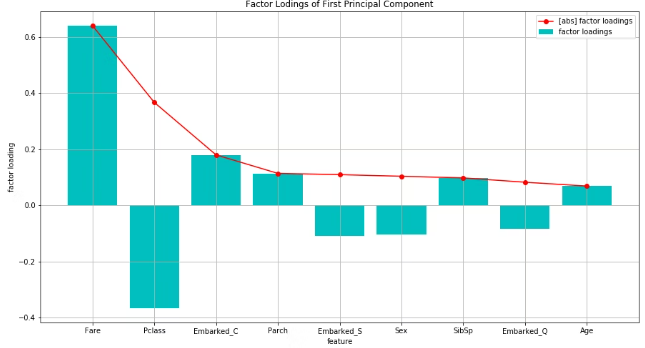
plt.show()

因子負荷量を見ると、絶対値(折れ線)としては、Fare(乗船料金)が一番高く、次にPclass(乗客の階級)が高い。
Pclassに差をつけて、他は大体同じくらい小さい。
第一主成分は、”裕福度を評価する指標”と考えることができそうである。

上記で確認した固有ベクトルと比較すると、Fareについて、固有ベクトルでは圧倒的に１番大きかったが、因子負荷量ではそこまでの差をつけていない。
また、Ageについて、固有ベクトルでは２番目に大きかったが、因子負荷量では最下位。
FareとAgeは、分散が大きいようだ。

主成分得点と各変数の相関を、固有ベクトルから判断しようとしてたら、
見誤ってしまうところであった。
因子負荷量を算出して確認すべきだ。

まとめ

主成分分析を行った結果、”裕福度を評価する”指標が得られ、
その指標が最も客(各データ)を分けられる(バラつかせる)ものであった。

また、固有ベクトルと因子負荷量で傾向が異なることを発見した、
これは、「(主成分の内容を確認するために)主成分と各変数の相関を見るときは、因子負荷量を見ること。固有ベクトルだけで判断すると、(分散の大きさに影響されているため)誤解を招く可能性がある」という注意点があるということだ。