概要
ベイズ最適化のライブラリを使って、
実際、良い感じに最適化ができるのか試してみました。
使用するライブラリは「GPyOpt」です。
理論について参考としたのは、下記書籍です。
「ガウス過程と機械学習」(著者: 持橋大地、 大羽成征)
実験概要
目的関数を作成し、その最小値(指定する定義域内)をベイズ最適化で求める。
詳細設定は下記の通りです。
– ベイズ最適化ライブラリ : GPyOpt (.methods.BayesianOptimization)
– 目的関数 :
y=f(x)=(x-300)(x-200)(x-15)(x-5)(x+6)(x+10)(x+100)
– 最適化の方針 : 最小化
– 定義域(x) : [-100 , 300]
– 獲得関数 : EI (改善期待値)
– 初期データ(x,y) :
x=−50,0,50,100,150,200,250
– カーネル : 未指定。(ライブラリのデフォルト設定は調べ切れておりません。)
今回はカーネルは置いといて、結果を見ます。
前提
- ベイズ最適化
ガウス過程回帰を用いて、目的関数の最小値(最大値)を求める手法。
ガウス過程回帰より得られた予測(確率分布)に対して、
獲得関数を適用し、その関数値が最大になる点を次点として探索していく。
- ガウス過程回帰
ベイズ推定の一種。\\
各入力点xに対する目的関数値f(x)を一つ一つ確率変数と見なし、\\
( f(x_{1}) , f(x_{2}) , … , f(x_{n}) , …) \\
を、多変量正規分布 N(μ , Σ) と見なす。\\
\\
取得済みの入力点を\\
x_{1} , x_{2} , … , x_{n}\\
とした時、新たな入力点の目的関数値(正規分布)を\\
f(x_{n+1}) 〜 p( f(x_{n+1}) | x_{n+1} , f(x_{1}) , f(x_{2}) , … ,f(x_{n}) )\\
と見なす回帰手法。\\
\\
目的関数値(正規分布)の期待値を予測値とする形で用いられたりする。\\
(上記のような関数 f を「ガウス過程」と呼ぶ。)\\- カーネル
ガウス過程回帰にて、\\
( f(x_{1}) , f(x_{2}) , … , f(x_{n}) , …)\\
の分散共分散行列 Σ の各成分の指定用関数。\\
\\
(i , j)成分、つまり、f(x_{i}) と f(x_{j}) の共分散を\\
x_{i} と x_{j} に依存する関数 k(x_{i} , x_{j}) で定め、 \\
その関数 k を「カーネル」と呼ぶ。\\
\\
一般に使われるカーネルはいくつか存在するが、\\
基本性質としては、\\
"入力点 x_{i} , x_{j} が近ければ、f(x_{i}) , f(x_{j}) も近い。" \\
実験詳細
1. ライブラリインポート
#pip install Gpyopt
import GPyOpt
import matplotlib.pyplot as plt
import numpy as np2. 目的関数
#目的関数定義
def f(x):
y = (x-300)*(x-200)*(x-15)*(x-5)*(x+6)*(x+10)*(x+100)
return y
#定義域の定義
xlim_fr = -100
xlim_to = 300
#グラフ
x = [i for i in range(xlim_fr , xlim_to + 1)]
y = [f(_x) for _x in x]
figsize = (10 , 5)
fig , ax = plt.subplots(1 , 1 , figsize=figsize)
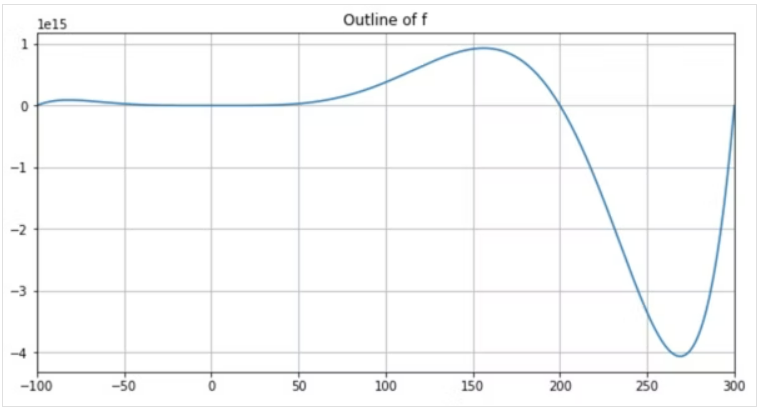
ax.set_title('Outline of f')
ax.grid()
ax.plot(x , y)
ax.set_xlim(xlim_fr , xlim_to)
plt.show()グラフより、定義域内では、
x が 270 あたりで最小値をとる形のようだ。
ベイズ最適化によって、その点が得られるか確認する。
3. 初期データ
#初期データ
init_X = [i for i in range(-50 , 300 , 50)]
init_X_np = np.array(init_X).reshape((len(init_X) , 1))
init_Y = [f(i) for i in init_X]
init_Y_np = np.array(init_Y).reshape((len(init_Y) , 1))
print(len(init_X))
print(len(init_Y))
print(init_X_np[:5])
print(init_Y_np[:5])
#初期データの位置をplot
figsize = (10 , 5)
fig , ax = plt.subplots(1 , 1 , figsize=figsize)
ax.set_title('Outline of f and Initial Data')
ax.grid()
ax.plot(x , y , label="f" , color="y")
#初期データ
for init_x , init_y in zip(init_X , init_Y):
ax.plot(init_x , init_y , marker="o" , color="r")
ax.set_xlim(xlim_fr , xlim_to)
plt.show()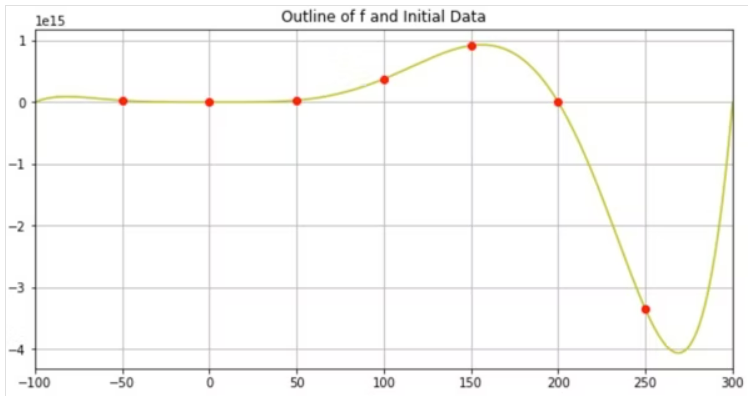
4. ベイズ最適化_モデル初期化
# 定義域
bounds = [{'name': 'x', 'type': 'continuous', 'domain': (xlim_fr,xlim_to)}]
# X , Y : 初期データ
# initial_design_numdata : 設定する初期データの数。上記 X , Yを指定した場合は設定不要。
# normalize_Y : 目的関数(ガウス過程)を標準化する場合はTrue。(今回は予測を真値と比較しやすくするためFalse)
myBopt = GPyOpt.methods.BayesianOptimization(f=f
, domain=bounds
, X=init_X_np
, Y=init_Y_np
, normalize_Y=False
, maximize=False
#, initial_design_numdata=50
, acquisition_type='EI')5. ベイズ最適化_train
myBopt.run_optimization(max_iter=10)6. ベイズ最適化_学習結果・過程
# 得られた最適解
x_opt = myBopt.x_opt
fx_opt = myBopt.fx_opt
print("x_opt" , ":" , x_opt)
print("fx_opt" , ":" , fx_opt)
# 最適化の軌跡
print("X.shape" , ":" , myBopt.X.shape)
print("Y.shape" , ":" , myBopt.Y.shape)
print("-" * 50)
print("X[:5]" , ":")
print(myBopt.X[:5])
print("-" * 50)
print("Y[:5]" , ":")
print(myBopt.Y[:5])

7. 予測_グラフ化
# ガウス過程回帰モデル
model = myBopt.model.model
#予測(第一成分:mean、第二成分:std)
np_x = np.array(x).reshape(len(x) , 1)
pred = model.predict(np_x)
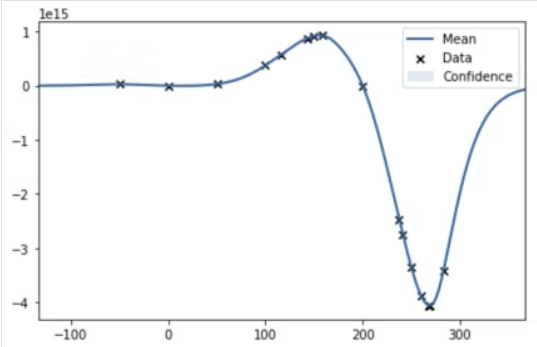
model.plot()
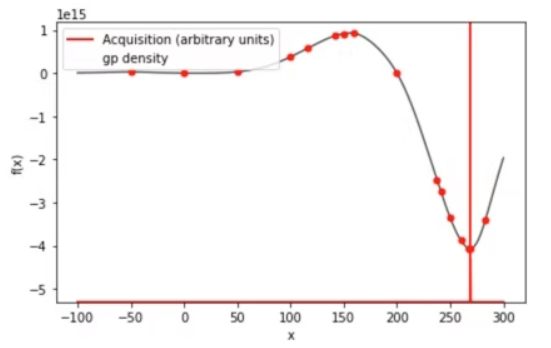
myBopt.plot_acquisition()
model.plot()
plt.plot(x , y , label="f" , color="y")
plt.plot(x_opt , fx_opt , label="Optimal solution" , marker="o" , color="r")
plt.xlim(xlim_fr , xlim_to)
plt.legend()
plt.grid()
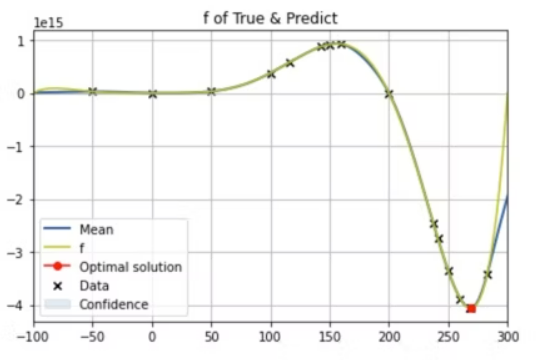
plt.title("f of True & Predict")
plt.show()3つ目のグラフにおける赤点が、得られた最適解である。
グラフを見るに最小値をちゃんと見つけられている形となった。
まとめ
(詳細な誤差は置いといて、)
ベイズ最適化によって実際に最小値を求めることができた。
ただ、今回は初期データとして、
x=250x=250 という最適解(最小値)に近い値を取っており、
それで最適化しやすい形になったかもしれない。
初期データが、”最適解から離れたデータのみ”であったら、
試行回数を増やす必要があるかもしれない。