F検定

初めに

今回は (t検定の次によく使われる感じである) F検定について説明します。
F検定の一例を取り上げ、検定の基本含めF検定がどんなものか、概要レベルで理解いただく目的で説明します。

「F検定」とは

F検定とは、「データを”F分布に従う形に”集計したものを用いる検定」であり、色々なケースで利用されています。
※「検定」については、下記で説明しています。

「F分布」とは

※F分布について下記2点を説明します。F検定の概要を学ぶ上で、[1.数式]は飛ばしても(詳細の話になるので)大丈夫です。ただ、[2.グラフ]は、ざっくりでもイメージを頭に残しておいた方が良いです。

1. 数式 (確率密度関数)
2. グラフ (t分布)

数式 (確率密度関数)

t分布の定義(f)は下記の通りです。
パラメータ( k_1 , k_2 )が2つ存在し、自由度と呼ばれています。(正の整数)
(Γは「ガンマ関数」と呼ばれる関数です。この関数の説明は、長くなるので省略します。)

f(x) = \frac{\Gamma(\frac{k_1+k_2}{2})x^{\frac{k_1-2}{2}}}{\Gamma(\frac{k_1}{2})\Gamma(\frac{k_2}{2})(1+\frac{k_1}{k_2}x)^\frac{k_1+k_2}{2}}(\frac{k_1}{k_2})^{\frac{k_1}{2}}

定義としては上記の通りですが、よく用いられる(F分布の)性質として下記があります。

W_1,W_2が自由度k_1,k_2のカイ二乗分布に従い、W_1とW_2が独立の時、\\\\
f(x) = \frac{(\frac{W_1}{k_1})}{(\frac{W_2}{k_2})}
\\\\
= \frac{k_2}{k_1}\frac{W_1}{W_2}

つまり、取得データからカイ二乗分布に従うような集計を2種類行えれば、F分布に従う集計が行えます。

グラフ (F分布)

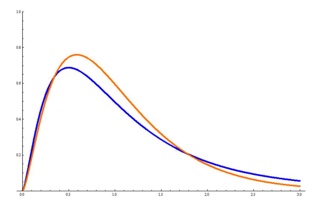
F分布のグラフは下図の通りです。
青と橙共にF分布であり、青の自由度が(5,10) 、橙の自由度が(5,100)です。
F検定では、帰無仮説を仮定した上で、F分布に従う形にデータを集計し、“その集計値が指定基準より大きい”場合に帰無仮説を棄却します。
(カイ二乗検定と同じですね。)

「F検定」の例

等分散性の検定 (対応の無い2群の検定)

初めに

本例について、この記事では数学の観点で説明をします。
検定結果の見方については、下記記事を参照ください。

検定概要

端的に言うと、「2群の母分散が等しいか否か」を調べる検定になります。
AグループとBグループの数値結果が、”同じバラツキ度合い“であるかを調べます。
帰無仮説と対立仮説は下記の通りです。

帰無仮説 H_0 : σ^2_A = σ^2_B \\\\
対立仮説 H_1 :  σ^2_A ≠ σ^2_B \\\\
※ σ^2_A(σ^2_B) : グループA(B)の母分散

検定で使用する集計値(F値)

本検定では、F分布に従う形にデータを集計し、その集計値が分布的に所謂”稀”であるか否かを調べます。

今から集計方法を説明します。
先に前提の話ですが、各群の分布は”独立な正規分布”と仮定して集計を行います。
そして、前準備の集計として、下記集計を行います。
正規分布とカイ二乗分布の性質より、下記で独立なカイ二乗分布が作成できます。

【前準備①】カイ二乗分布(自由度:n_A-1)の作成 (A群)\\\\
W_A = \dfrac{\sum_{i=1}^{n_A}(x_{Ai} - \bar{x_A})^2}{σ_A^2}

【前準備②】カイ二乗分布(自由度:n_B-1)の作成 (B群)\\\\
W_B = \dfrac{\sum_{i=1}^{n_B}(x_{Bi} - \bar{x_B})^2}{σ_B^2}

前準備①②を利用し、以下の通りに集計を行います。
この集計結果がF分布に従う形になり、本検定で利用するものになります。

F分布(自由度 : n_A-1 , n_B-1)の作成\\\\
※帰無仮説を仮定するため、
σ^2_A = σ^2_B\\\\
F = \frac{(\frac{W_A}{n_A-1})}{(\frac{W_B}{n_B-1})}
\\\\
= \frac{n_B-1}{n_A-1}\frac{W_A}{W_B}

前提として、検定は、「帰無仮説を仮定した時に集計値が”分布的に稀かどうか”を調べる」ものです。
今回の検定の帰無仮説は「母分散が等しい」なので、カイ二乗分布の割り算を行った結果、両方の母分散が消え、集計可能な形になります。
“この集計結果(F値)が分布的に所謂稀なデータか？“で“帰無仮説を棄却するか否か“を判断します。

最後に

F分布 / t分布 / カイ二乗分布 / 正規分布は、検定でよく用いられるものであり、且つ、関連度合いが高いです。
上記や各種検定の記事で[数式 (確率密度関数)]に”他分布との性質“を記載しましたが、それら性質は、統計学の理解を深める上で重要です。
しっかり押さえておきましょう。