初めに
t検定(※)に並び、統計の仮説検定でよく用いられるものとしてχ二乗検定があります。
今回はその一例を見て、χ二乗検定がどんなものか、概要レベルで理解いただく目的で説明します。
※t検定については以下の記事を参照ください。
「χ二乗検定」とは
χ二乗検定とは、「データを”χ二乗分布に従う形に”集計したものを用いる検定」であり、色々なケースで利用されています。
※「検定」については、下記で説明しています。
「χ二乗分布」とは
※χ二乗分布について下記2点を説明します。χ二乗検定の概要を学ぶ上で、[1.数式]は飛ばしても大丈夫です。(詳細の話になるので。)
ただ、[2.グラフ]は、ざっくりでもイメージを頭に残しておいた方が良いです。
- 数式 (確率密度関数)
- グラフ (χ二乗分布)
数式 (確率密度関数)
χ二乗分布の定義(f)は下記の通りです。
パラメータ( n )が1つ存在し、自由度と呼ばれています。(正の整数)
(Γは「ガンマ関数」と呼ばれる関数です。この関数の説明は、長くなるので省略します。)
f(x) = \frac{1}{2^\frac{n}{2}\Gamma(\frac{n}{2})}(x^2)^{\frac{n}{2}-1}e^{-\frac{x^2}{2}}定義としては上記の通りですが、よく用いられる(χ二乗分布の)性質として下記があります。
Z_i(i=1,...,n)が標準正規分布に従い、それらが互いに独立の時、\\\\
f(x) = \sum_{i=1}^{n}Z_i^2つまり、取得データから正規分布に従うような集計を行えれば、χ二乗分布に従う集計が行えます。
グラフ (χ二乗分布)
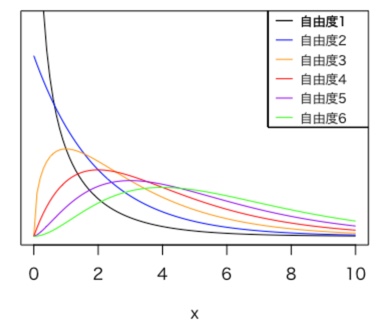
χ二乗分布のグラフは下図の通りです。
xの範囲は0以上であり、自由度によって形状が異なります。
特に”自由度3から山の形状になってる“のが大きな変化ではないでしょうか。
χ二乗検定では、帰無仮説を仮定した上で、χ二乗分布に従う形にデータを集計し、”その集計値が指定基準より大きい”場合に帰無仮説を棄却します。
「χ二乗検定」の例
適合度の検定
概要
χ二乗検定の中で比較的知名度が高いと思われる検定です。
適合度の検定はざっくりいうと、”確率分布が特定の分布であるか?“を検証するものです。
少しざっくりし過ぎてイメージが湧かないかもしれません。
具体例を出しましょう。
少し歪になった(かもしれない)サイコロ(目は1~6)があったとして、”このサイコロの各目の発生確率が同じ(1/6)であるか?“を検証するのが、本検定の1例です。
帰無仮説 / 対立仮説
各仮説は下記の通りに設定します。
上記具体例の場合、帰無仮説は、「サイコロの各目の確率が1/6である」と設定します。
帰無仮説:「各発生事象(n個)の確率が\hat{p}_i(i=1,...,m)である。」\\\\
対立仮説:「各発生事象(n個)の確率が\hat{p}_i(i=1,...,m)でない。」\\\\
※\hat{p}_i(i=1,...,m):特定の確率値入力データ / カイ二乗値
本検定で使用する入力データは、「実際に試行を行った結果、各事象は何回発生したか?」という情報を使います。
上記から使ってる具体例(サイコロ)で考えると下表のようなデータです。
| 1の目 | 2の目 | 3の目 | 4の目 | 5の目 | 6の目 | |
| 発生回数 | 5 | 9 | 2 | 10 | 5 | 6 |
入力データを用いて、カイ二乗分布に従う形に集計を行います。
“集計結果(カイ二乗値)が分布的に所謂稀なデータか?“で”帰無仮説を棄却するか否か“を判断します。
過程は難しい話になるので結論だけ説明しますが、下記の集計でカイ二乗値が作成できます。
観測結果Oと期待値Eを、上記の具体例(サイコロ)で考えると、0は上表の発生回数であり、Eは全て n/6 となります。
各事象(n個)の発生回数について、\\\\
観測結果をO_i(i=1,...,n)、\\\\
(帰無仮説を仮定した時の)期待値をE_i(i=1,...,n)とした時、\\\\
χ^2_0=\sum_{i=1}^{n}\frac{(O_i-E_i)^2}{Ei}〜\chi^2(n-1)最後に
カイ二乗検定もt検定と同様に、検定としては頻出です。
上記の”カイ二乗分布が標準正規分布の二乗和で表せる“という性質は、統計学を深掘りするにあたって重要なポイントです。
性質と分布形状は特に押させておきましょう。