初めに
統計の仮説検定でよく用いられるものとしてt検定があります。
今回はその一例を見て、検定の基本含めt検定がどんなものか、概要レベルで理解いただく目的で説明します。
「t検定」とは
t検定とは、「データを”t分布に従う形に”集計したものを用いる検定」であり、色々なケースで利用されています。
※「検定」については、下記で説明しています。
「t分布」とは
※t分布について下記2点を説明します。t検定の概要を学ぶ上で、[1.数式]は飛ばしても大丈夫です。(詳細の話になるので。)ただ、[2.グラフ]は、ざっくりでもイメージを頭に残しておいた方が良いです。
- 数式 (確率密度関数)
- グラフ (t分布)
数式 (確率密度関数)
t分布の定義(f)は下記の通りです。
パラメータ( k )が1つ存在します。(正の整数)
(Γは「ガンマ関数」と呼ばれる関数です。この関数の説明は、長くなるので省略します。)
f(x) = \frac{\Gamma(\frac{k+1}{2})}{\sqrt{k\pi}\Gamma(\frac{k}{2})(1+\frac{x^2}{k})^\frac{k+1}{2}}定義としては上記の通りですが、よく用いられる(t分布の)性質として下記があります。
Nが標準正規分布、Wがカイ二乗分布(自由度k)に従い、NとWが独立の時、\\\\
f(x) = \frac{N}{\sqrt{\frac{W}{k}}}つまり、取得データから正規分布とカイ二乗分布、それぞれに従うような集計を行えれば、t分布に従う集計が行えます。
グラフ (t分布)
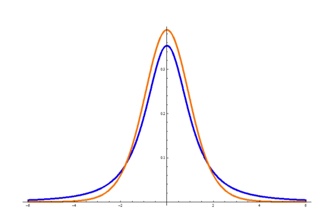
t分布のグラフは下図の通りです。
青と橙共にt分布であり、自由度は青より橙の方が大きいです。
見ての通り、正規分布と同じように、左右対称の釣鐘状になっていて、自由度が高くなるにつれて裾野が狭くなります。
そして、自由度が限りなく∞に近づく時、t分布は正規分布に近づきます。
t分布を使用するメリット/デメリット
上記の通り、t分布は正規分布と似た形状をしています。
「t分布は複雑な数式だし比較的有名でもないため、t分布より正規分布を使って検定した方が良くない?」という意見が出てくるかもしれません。
その点について、t分布を利用するメリット/デメリットは、(筆者の思惑に過ぎませんが、)下記の通りだと考えております。
【メリット】
未知のパラメータがあっても利用できる。
→一例として、”平均に対する検定“を考える時、(標準)正規分布を用いて検定を行う場合は分散のパラメータσ^2が既知である必要があります。一方、t分布は上記の通り正規分布とカイ二乗分布の割り算であり、上手いこと”σ^2を考えなくて良い”形にできます。
【デメリット】
分布的に結果の納得感が出づらい
→上記説明の通り、t分布は正規分布に比べて裾野が広いです。なので、例え帰無仮説が正しかったとしても、集計結果が”分布の中心から外れる”可能性が比較的高く、その逆も然りです。
「t検定」の例
平均値の検定
例として、下記の検定の説明します。
「取得データ x_i (i=1,...,n) の平均が特定値 μ であるか?\\\\ 但し、データの母分散σ^2は未知である。」
ちなみに、”母分散既知のケース”については以下の記事で説明しています。
母分散既知のケースならば上記記事の通り正規分布で検定が行えますが、今回は正規分布ではできません。
今回はt分布を用いて検定を行うことができます。
t分布の集計を行う前準備(知識)として、2種の集計を行います。
それぞれの集計方法・分布は下記の通りです。
【前準備①】標準正規分布の作成\\\\
Z = \dfrac{(\bar{x} - μ)\sqrt{ n }}{σ}【前準備②】カイ二乗分布(自由度 : n-1)の作成\\\\
W = \dfrac{(n-1)s^2}{σ^2}\\\\
但し、s^2 = \frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n-1}上記2種の集計結果Z,Wを用いて、下記の通り、t分布に従う集計が行えます。
t分布(自由度 : n-1)の作成\\\\
t = \dfrac{Z}{\sqrt{\frac{W}{n-1}}}\\\\
= \dfrac{\bar{x}-μ}{\sqrt{\frac{s^2}{n}}}正規分布とカイ二乗分布それぞれでσが出てきましたが、割り算のおかげでσが未知でも集計が可能な形になりました。
このt分布に従う集計結果を用いて、取得データが”確率的に稀”(=分布の中心から外れてるか?)を確認する形で行います。
最後に
上記説明の通り、検定では正規分布に比べ、t分布の方が利用可能ケースが多いです。
t分布の式(確率密度関数)は複雑なので、t分布の形状や利用理由から理解を進めていくと良いと思います。