概要
決定木 (デシジョンツリー) は、分類モデルの一種です。
但し、「回帰木」と呼ばれる、回帰に適用したものもあります。
ですが、今回は分類モデルの方に注目して説明します。
“分類するにあたって良い感じにデータ分割できる基準値を見つけて、データを分割する“事を階層的に繰り返し、モデルが作成されます。
※本記事では、「分割」と「分類」の意味を下記の通りに使い分けています。「分類」はモデルの目的である目的変数(カテゴリ)を予測する事であり、「分割」は上記「分類」を行うためにモデル学習で行うデータ分割を指しています。
決定木は、下図のように、分類基準や件数割合(分類クラス別)の可視化がしやすく、説明力が高い(=モデル内容が分かりやすい)です。
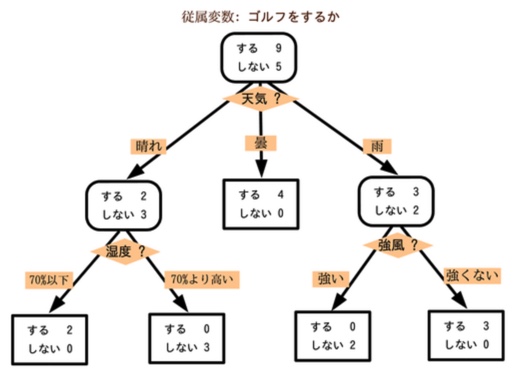
上図における(角丸)四角は「ノード」と呼び、一番下に紐づいている末端のノードを「葉」と呼びます。
各ノードには(分割後の)データを表しており、(上図では)四角の中に分類対象のクラス別データ件数が表示されています。
上記で「良い感じにデータ分割できる基準値を見つけて〜」と記載しました。
「良い感じ」とは、「データが特定の分類クラスに偏るように」という意味です。
背景として、「特定の分類クラス(A)に偏る」ことは「このデータ特性(分割)はクラスAの特性と見なし、その特性を持つデータはクラスAと予測するのが妥当」と考えてる形になっています。
詳細
モデル学習フロー
モデル学習では、「情報利得」という指標を使います。
詳細は下記で説明しますが、「情報利得」は、”対象の分割によって、どの程度良い感じに分類ができるか“を数値化したものです。
決定木において、モデル学習は”上図の木構造を作成すること“です。
学習の流れは下記の通りです。
- 学習データ全体に対して、情報利得が最大になるデータ分割方法を探し、その方法でデータを分割する。
- 分割した各データ群それぞれに対して、情報利得が最大になる分割方法を探し、データ分割を行う。
- 以上の流れでデータを分割していき、木構造を作る。「どこまで分割するか?」ですが、「情報利得が無い」や「ハイパパラメータで指定した分割回数」等のタイミングで終了します。
- 完成した木構造における葉(末端)のデータは、「最もデータ件数の多い分類クラス」のデータと考え、その特性を予測時の判断基準とする。
情報利得
情報利得は「不純度」という指標を用いて算出されます。
詳細は下記で説明しますが、不純度は「対象データにおける分類クラスの偏り度合い」を数値化したものです。
偏っている、つまり、分類クラスの予測がしやすい場合は小さい値になり、偏っていない、つまり、分類クラスを予測しずらい(不純)場合は大きい値になります。
※不純度は、上記より「情報の曖昧さ」と表現することがあります。
情報利得は下記の式で算出されます。
分割前に比べて不純度がどれだけ減ったか(=どれ程情報を得たか)を計算している形です。
分割後の不純度は、「分割後の各データ群における不純度の平均」としています。
※不純度は英語で imputity であり、情報利得は Imformation Gain です。
分割前のデータ(件数:N)に対する不純度をI(D) 、\\\\
分割後のデータ群に対する不純度をI(D_{k})とする。\\\\
(k=1,2,...,m)\\\\
且つ、データ群kの件数はN_kとする。\\\\
この時、対象の分割による情報利得IGは下記の通り。\\\\
\\\\
IG = I(D) - \sum^{m}_{k=1}\frac{N_k}{N}I(D_{k})不純度
上記「情報利得」の説明で概要説明した通りです。
不純度として用いられる指標はいくつか存在し、(分類モデルとしての)決定木でよく用いられる指標は下記2つです。
- (情報)エントロピー
- ジニ係数
どちらも、不純度として相応しい下記点を満たしています。
- 「一つの分類クラスのデータのみ」ならば「値は最小(=0)」
- 「各分類クラスのデータが同じ件数存在」ならば「値は最大」
情報エントロピー
決定木において、情報エントロピーは下記式で算出されます。
情報エントロピーは、応用数学である「情報理論」で注目される尺度になります。
対象ノードのデータ件数をN、分類クラスの数をlとし、\\\\
クラスhのデータ件数をN_{h}とする。\\\\
※N=\sum^{l}_{h=1}N_h\\\\
対象のデータ・分類クラスにおける情報エントロピーI_H(D)は下記の通り。\\\\
\\\\
I_H(D) = -\sum^{l}_{h=1}\frac{N_h}{N}log_2\frac{N_h}{N}ジニ係数
決定木において、ジニ係数は下記式で算出されます。
ジニ係数は、所得格差を測る指標(※1)として経済学等でも使われています。
(※1)数完全平等線とローレンツ曲線で囲まれた面積の2倍。
対象ノードのデータ件数をN、分類クラスの数をlとし、\\\\
クラスhのデータ件数をN_{h}とする。\\\\
※N=\sum^{l}_{h=1}N_h\\\\
対象のデータ・分類クラスにおけるジニ係数I_G(D)は下記の通り。\\\\
\\\\
I_G(D) = 1-\sum^{l}_{h=1}(\frac{N_h}{N})^2