概要
分散分析をSASで実施し、数値を見てみます。
分散分析については以下の記事を参照いただければと思います。
本記事もシンプルな”一元配置“分散分析を行ってみます。
【SAS】実装方法
SASでは、glmプロシージャで分散分析ができます。
(「glm」は「一般化線形モデル」の略称であり、上記プロシージャは名前通り、一般化線形モデルも実行できるものです。)
下記の形で実装することで分散分析が行えます。
[グループ変数]には、因子となるカテゴリ値変数を指定し、[数値]には、分析対象となる数値変数を指定します。
「solution」は、指定することでモデル式のパラメータ推定値が出力されます。(本記事では確認対象外です。)
※モデル式については、下記「何で “regプロシージャと同じ数表” なのか?」を参照ください。
proc glm data=[データセット名];
class [グループ変数];
model [数値] = [グループ変数] / solution;
quit;【SAS】実装
実施概要
下記データを作成し、「グループA , B で数値に有意な違いがあるか?」を調べてみましょう。
データ
下記合計1,000件のデータを作成。
- グループAの数値 : 正規分布 (平均 -5 , 標準分散 5) の乱数で作成 (500件)
- グループBの数値 : 正規分布 (平均 5 , 標準分散 5) の乱数で作成 (500件)
想定する分析結果
上記の通り、グループ間で平均値が異なります。(5 と -5)
なので、分析結果としては「F値が大きい」形になり、「グループ間で有意な差がある」という結論になると想定できます。
実装
データ作成
data testdata;
keep category value;
seed = 20;
/* category = A */
num = 500;
_mean = -5;
_std = 5;
do i=1 to num;
category = 'A';
value = _mean + _std * rannor(seed);
output;
end;
/* category = B */
num = 500;
_mean = 5;
_std = 5;
do i=1 to num;
category = 'B';
value = _mean + _std * rannor(seed);
output;
end;
run;分散分析
proc glm data=testdata;
class category;
model value = category / solution;
quit;実行結果
データ作成
下記のようなデータが作成できます。(5件を表示)
| category | value |
| A | -4.0074 |
| A | 7.6716 |
| A | -7.1349 |
| B | 2.2678 |
| B | 0.8699 |
分散分析
複数のレポート(数表やグラフ)が出力されます。
その内、今回の確認ポイントは下図のレポートです。
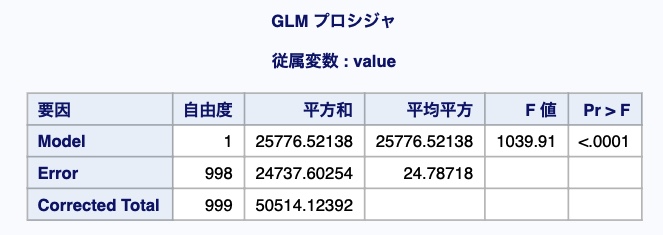
上図の右2列にF値とP値が載っています。
P値がとても小さいため、想定通り「グループ間で有意な差がある」と結論付けができます。
何で “regプロシージャと同じ数表” なのか?
上表を見て、「分散分析なのに群間分散と群内分散の表記が無い」ことに疑問を感じるかもしれません。
というのも、上表の行[Model]、[Error]ですが、線形回帰分析 (regプロシージャ) では、モデル平方和([Model])、残差平方和([Error])の位置付けで出力されます。
※モデル平方和 : 予測値と予測値平均の差の平方和
※残差平方和 : 目的変数値と予測値の差の平方和
上表は何故regプロシージャと同じ表なのでしょうか?
その疑問の回答は下記の通りです。
glmプロシージャでは、下記のモデル式で線形回帰分析をする形になっています。
その時、「モデル平方和」と「残差平方和」は、 「群間平方和」と「群内平方和」と一致します。
なので、(モデル平方和と残差平方和の比で算出された)F値は、分散分析のF値になるという事です。
故に、上表における行[Model]は「群間平方和」の行、行[Error]は「群内平方和」の行になります。
【glmプロシージャにおけるモデル式】\\\\
n個の数値データy_{ij}を下記モデルと仮定する。\\\\
iはグループの番号を意味し、\\\\
ε_{ij}は互いに独立な正規分布N(0 , σ^2)に従う。\\\\
y_{ij} = μ + α_{2}x_{2} + ... + α_{k}x_{k} + ε_{ij}\\\\
(※1)i=1,...,k、j=1,...,n_i\\\\
(※2)n=n_1+n_2+...+n_k\\\\
\\\\
x_tは、グループ番号がtの時に「1」となり、\\\\
それ以外の時は「0」になる2値変数。\\\\
\\\\
glmプロシージャでは、\\\\
yを目的変数、xを説明変数として\\\\
線形回帰を行ってるイメージになる。\\\\
結果、「グループ番号tの予測値」は、\\\\
「グループtの数値データ(目的変数)の平均」になる。