初めに
この記事では、SASで実際に線形回帰分析をし、グラフや数値を見てみます。
回帰分析を学び始めた方向けに、今回はシンプルな単回帰分析を行います。
※単回帰分析:説明変数1つで行う回帰分析。複数の説明変数を用いる場合は、「重回帰分析」と呼ぶ。
SASでは、(他の分析もですが、)線形回帰分析が簡単なコードで実行でき、且つ、分析結果として様々なレポートが出力されます。
線形回帰分析は特に様々な指標・グラフが出力され、今回はそれぞれを簡単に説明します。
※本記事は予測結果の吟味でなく、出力レポートの概要説明を行います。
「線形回帰分析」とは
簡単に言うと「特定の変数値を、他の変数(群)の線形結合で予測する」手法です。
詳細については、下記を参照ください。
SASコード
今回は下記の通りにコーディングしていきます。
- データセット作成(x,yの2変数)
- 散布図を出力
- 線形回帰分析
データセット作成(x,yの2変数)
多変量正規分布の乱数でデータを生成します。
※コードの詳細は(本題ではないので)省略します。
DATA data_xy;
KEEP x y;
/* パラメータ */
mux=2; muy=1; /* 母平均 */
varx=10; vary=50; /* 母分散 */
covxy=20; /* 母共分散 */
n=30; /* 標本の大きさ */
seed=1234; /* シード値 */
/* エラー処理 */
IF (vary-covxy**2/varx)<=0 THEN DO;
PUT 'ERROR:分散共分散行列が正定値(positive definite)ではありません。';
STOP;
END;
/* 乱数生成のためのループ */
DO i=1 TO n;
x = mux+SQRT(varx)*RANNOR(seed);
y = muy + covxy / varx* (x-mux) + SQRT(vary -covxy**2/varx)*RANNOR(seed);
OUTPUT;
END;
RUN;
散布図を出力
sgplotプロシージャで実行してみます。
scatter箇所は「x=[横軸の変数名] y=[縦軸の変数名]」という形式です。
proc sgplot data=data_xy;
scatter x=x y=y;
run;
quit;線形回帰分析
regプロシージャ線形回帰分析ができます。
model箇所は、「[目的変数] = [説明変数1] [説明変数2] … [説明変数p]」という形式です。
つまり、各説明変数はスペース区切りで指定する形です。
proc reg data=data_xy;
model y=x;
run;
quit;実行結果
実行結果は以下の通りでした。
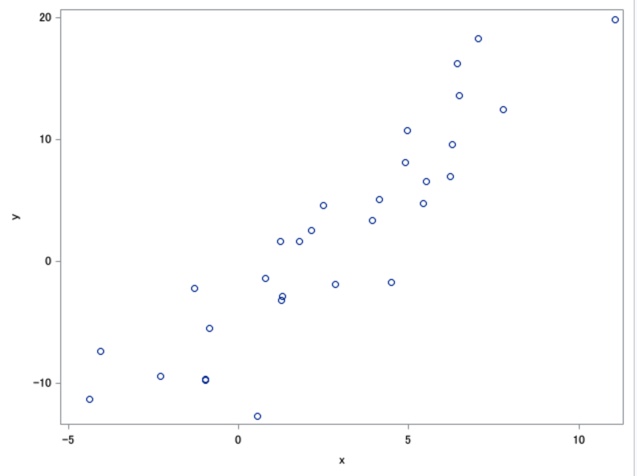
散布図
2変数がある程度相関を持つように乱数を生成した結果、線形回帰分析でいい感じに分析ができそうなデータになりました。
線形回帰分析
回帰性
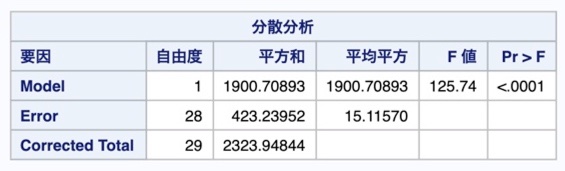
下表で、「回帰性が無いか?」の検定結果が確認できます。
具体的に言うと、「“説明変数に係る”回帰係数が全て 0 」(回帰性が無い)という帰無仮説の検定です。
統計量はF統計量であり、その結果(F値)は下図の「F値」です。
下図では、F値は125.4であり、P値(Pr>F)はごく僅かなので、帰無仮説は棄却され、「回帰性はある」と判断されます。
帰無仮説を仮定すると、F統計量は、下記の通りになります。
つまり、上図の「平均平方」の割り算で算出されます。
F(k-1,n-k)=\frac{(\frac{[回帰変動]}{k-1})}{(\frac{[残差変動]}{n-k})}\\\\
※n:データ数、k:回帰パラメータ数決定係数
決定係数は”モデルの当てはめの良さ“を測る尺度であり、値は、”0以上1以下“です。
決定係数は下図の通り、「R2乗」と「調整済みR2乗」の2種類があります。

「調整済みR2乗」は何か?ですが、端的にいうと、「説明変数の数が異なるモデルを比較する際に利用する」尺度です。
「R2乗」は”説明変数の数が増えれば値が同じ又は大きくなる“という性質があるので、説明変数の数でペナルティ(値を小さくする)を加えたのが「調整済みR2乗」です。
それぞれの尺度は下記計算式で算出されます。
[R2乗]=\frac{[回帰変動]}{[全変動]}\\\\
=1-\frac{[残差変動]}{[全変動]}\\\\
[調整済みR2乗]=1-\frac{(\frac{[残差変動]}{n-k})}{(\frac{[全変動]}{n-1})}\\\\各回帰パラメータの有意性
こちらは、各回帰パラメータ毎に実施された、「真パラメータが0」という帰無仮説のt検定です。
帰無仮説が棄却されれば、その回帰パラメータは優位である、つまり、”対象の説明変数には回帰性がある“と判断されます。

上図では、定数項(intercept)とx共に、t値が大きく、結果、P値(Pr>|t|)がごく僅かになっています。
よって、どちらの回帰パラメータも帰無仮説が棄却され、”有意である“と判断されます。
残差 – 予測値のプロット
表題の通り、各データについて、縦軸を残差、横軸を予測値でプロットしたものです。
前提として、線形回帰分析で求められた予測値と残差は無相関(内積0)になります。
なので、プロットの結果、前提に反して相関性が”ある”感じの場合、”各データの分散が均一でない“や”回帰式がデータに合っていない“などが考えられます。
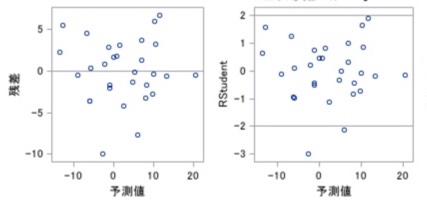
上図は、縦軸が”残差“か”標準化した残差“かの違いです。
残差の平均は0なので、つまりは、分散を1にスケーリングしたか否かの違いです。
左図が”残差“、右図が”標準化した残差“です。
L-Rプロット
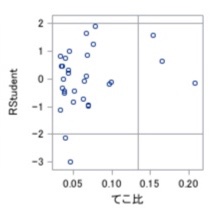
標準化残差(Residual)、てこ比(Leverage)のプロットです。
残差は”目的変数の外れ値“(=予測値との外れ度合い)、てこ比は”説明変数値の外れ値“(=平均との外れ度合い)になります。
線形回帰分析は説明変数値の外れ値に予測を寄せる性質があり、つまりは、縦軸又は横軸に大きい点(データ)は、モデルに悪影響を及ぼしてる可能性があります。
そのような点を見つけ、”そのデータを除外してモデル精度を上げる“等を行うために本プロットを確認します。
Q-Qプロット
線形回帰分析では、前提として、”各データは正規分布に従う“と考えています。
「その前提がそもそも正しいか?」を確認するために本図を確認します。
Q-Qプロット自体については下記ページを参照ください。
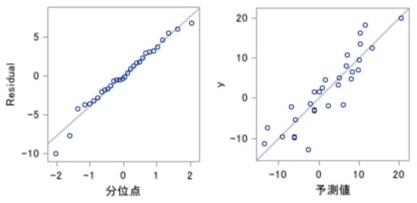
出力されるQ-Qプロットは下図の2つがあります。
左は残差、右は目的変数の正規Q-Qプロットです。
残差も目的変数も、上記前提の時は正規分布になるので、前提が正しければプロットは直線に近くなります。
クックのD
上記「L-Rプロット」は、y(目的変数)とx(説明変数)の外れ値を調べる図と説明しました。
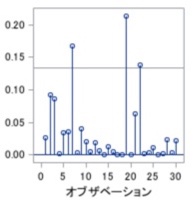
「クックのD」はデータ毎に算出される1つの尺度であり、”y又はxの外れ度合い“を測る尺度(0以上)です。
なので、値が大きいデータがあれば、「L-Rプロット」と同様に、除外などの対応を検討した方が良いと考えます。
最後に
上記の通り、線形回帰分析では様々なレポートが出力されます。
レポートの理解を深めるためには、線形回帰分析の前提・導出過程などの理解が前提として必要になります。
大変かもしれませんが、理解を深めることで、結果的に、(説明性の高い)線形回帰をより良いモデルへ改善できるようになっていくと思います。