回帰分析において、目的変数を(そのまま使うのではなく、)対数変換してモデリングを行った時、どのような解釈ができるでしょうか?
どういう話?
簡単に、数式でいうと、
y = ax +b
ではなく、
log(y)=ax+b
を用いる場合、得られたパラメータa の解釈についての話です。
結論
log(y)=ax+b\\ の形式で回帰分析を行って 得られる回帰パラメータaは、\\ 「xが1増えるとyが(1+a)倍になる」\\ と解釈できる。言い換えると、\\ 「xが1増えるとyが(a*100)\%増える」\\ と解釈できる。\\ \\ ※但し、上記解釈ができるのはaが0付近の時。
何故か?
上述の回帰式で考えます。\\得られた回帰パラメータa.bに対して、\\ x_0,y_1,y_2を\\ log(y_1)=ax_0+b\\ log(y_2)=a(x_0+1)+b\\ が成り立つ値とします。\\ \\ つまり、xが1増えた時の左辺の増加量は、\\ log(y_2) - log(y_1)(=a)\\ です。それが何故、上述の結論になるのでしょうか?
上述の式を変形すると、\\
log(y_2)-log(y_1) = log(y_2/y_1)\\
=log(1+\frac{y_2-y_1}{y1})=a\\
となります。\\
\\
ここで、(本題から少し離れ、)\\
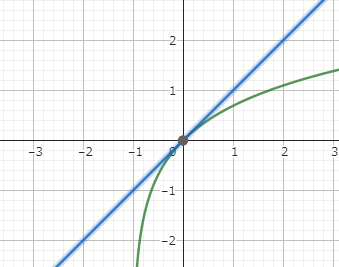
f(t)=log(1+t)とg(t)=tという関数を考えます。\\
これら関数は下図の通り、t=0付近では大変近い値になります。\\
つまり、t=0付近では\\
log(1+t)≒t\\
と見なせると考えます。\\
\\
以上をまとめると、下記の関係になるので上述の結論となる。\\
a=log(1+\frac{y_2-y_1}{y_1})\\
≒\frac{y_2-y_1}{y_1} \\