前提
「線形回帰モデル」を説明する前に、前提として必要な事を説明致します。
予測モデル
ざっくりな意味合いとして説明します。
予測モデルは、「特定の変数値(※1)を、他の変数(※2)を用いて予測するモデル」を指します。
具体的なイメージを掴んでいただくために、“購買に関する”予測モデルを例に取り上げてみましょう。
この予測モデルでは、”(日別の)アイスの売上“を上記(※1)としましょう。
モデルの利用目的としては、”予測結果を見て、無駄の無い発注を行う“等が考えられます。
この時、”上記(※2)のデータをどうするか“ですが、”アイスの売上“に関連しそうなものを考える事が自然でしょう。
例えば、下記が挙げられるかと思います。
- 曜日
- 祝日か否か
- 気温
- 湿度
- 前日の売上
- プロモーション中の商品カテゴリ
次に予測モデルの作成方法について説明します。
ざっくりな流れは下記の通りです。
- 過去の(※1)、(※2)を用意する。
- 学習手法を決める。(※3)
- 上記 1. と 2. のデータ・手法で、(※1)と(※2)のパターンを抽出する。(モデル学習)
- 上記 3. で出来上がったモデルを、”上記 1. とは別の” 過去データ(※2)を用いて予測し、(※1)と予測結果が良い感じに合っているか調べる。(モデル検証)
- 上記 4. の比較結果が悪ければ、モデル学習データの追加・削減や手法変更を行い、再度上記 3. と 4. を繰り返す。
- 上記 4. の結果が良い感じであれば、モデルの出来上がり。
今回説明する「線形回帰モデル」は、上記手順 2. の手法の一つです。
目的変数・説明変数
上記 [ 予測モデル ] における (※1) を 「目的変数」、(※2) を 「説明変数」と言います。
線形結合
数学用語です。
簡単に言うと、「定数倍した各変数の和」です。
例えば、x , y を変数、a , b を定数とした時、(ax + by) が “xとyの線形結合” となります。
上記の線形結合をzとし、3次元空間で表現すると、直線(線形)になります。
「線形回帰モデル」の概要
「線形回帰モデル」は端的に言うと、「目的変数を、説明変数の線形結合で予測する」モデルです。
目的変数を y_i、説明変数をx_{ij}、予測結果を\hat{y}_iとする。(i:1〜n 、 j:1〜m)\\\\
線形回帰モデルは、予測結果\hat{y}_iを下記の通りに設定する手法。\\\\
\hat{y}_i=\sum^{m}_{j=1}β_jx_{ij}\\\\
上式のβ_jは、(ざっくり言うと)\\\\
"n個のデータ(y_i , x_i1,...,x_im)に対して適する定数"であり、\\\\
モデル学習の際にデータ集計をして決定する。説明変数が1変数の場合、グラフは下記のようになります。
横軸が説明変数で縦軸が目的変数、赤点がデータであり、予測結果が青線です。
線形回帰モデルでは、”予測結果を、説明変数の線型結合で表現する“モデルなので、下図の通り、予測結果は直線になります。
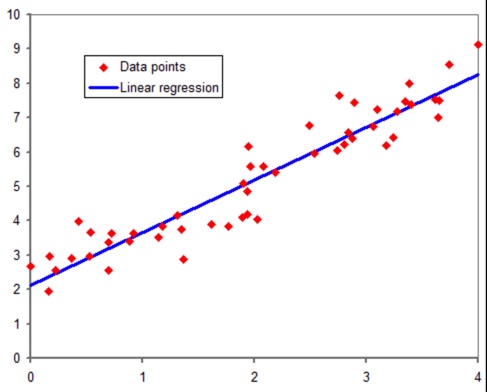
線形モデルの”モデル学習“では、線型結合で使用する定数 β_j (j=1,…,m)を決定します。
※「パラメータ(β)を推定する」と表現されたりします。
“どのようにして決定するか?”は、下記にて説明します。
「線形回帰モデル」の詳細
パラメータβの求め方
上記の通り、線形回帰モデルのモデル学習で行うことは”データに適しおたパラメータβ_jを求める“です。
求め方は大別すると下記2通りが存在します。
- 最小二乗法
- 最尤法
それぞれの概要を下記に記載します。
最小二乗法
最小二乗法は、「目的変数と予測結果の二乗和が最小になるβを求める」手法です。
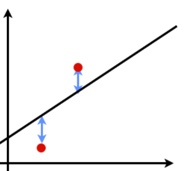
下図は、データ(赤点)と予測結果(直線)です。
青線は、ご覧の通り、”データと予測結果の差“(=「残差」)を意味しています。
この”青線の長さの(二乗)和”(=「残差平方和」)を最小にするβを求めるのが最小二乗法です。
数式で表すと下記の通りです。
目的変数を y_i、説明変数をx_{ij}、予測結果を\hat{y}_iとする。(i:1〜n 、 j:1〜m)\\\\
最小二乗法は、"残差平方和を最小にするβを求める"手法です。\\\\
[残差平方和]=\sum^{n}_{i=1}e^2=\sum^{n}_{i=1}(y_i-\hat{y}_i)^2
最尤法
最尤法は、「目的変数を確率変数と見なし、データ値の確率を最大にするβを求める」手法です。
確率的に考える手法なので、最小二乗法に比べ、少し複雑かもしれません。
ですが、「線形回帰モデル」をより一般化した「一般化線形モデル」では、最尤法を用いる形であり、最小二乗法は「線形回帰モデル」でしか基本的には利用できません。
なので、理解を深める上で最尤法は避けて通れないものです。
最尤法の前提として、目的変数は(下記の通り)正規分布の確率変数と考えます。
その前提の上で、”取得データy_1,…,y_nの確率が最大になるβ“を求めます。
※最尤法は、他のモデルでも利用される手法であり、意味合いとしては、”取得データの出現確率が、最大(=最(尤)もらしい)であると捉えた時のパラメータ値を求める“手法です。
最尤法では、\\\\(基本的に)目的変数y_iの確率(密度関数)を下記の通りに定めます。\\\\
f(y_i) = \sum^{m}_{j=1}β_jx_{ij} +u_i\\\\
ここで、u_i(i=1,...n)は互いに独立な標準正規分布です。\\\\
βとxは固定値と考え、つまりは、y_iは下記の正規分布であると考えます。\\\\
y_i 〜 N(\sum^{m}_{j=1}β_jx_{ij} , 0)\\\\
\\\\
u_iが互いに独立のため、y_iも互いに独立となります。\\\\
なので、最尤法では下記の確率を最大にするβを求めます。\\\\
f(y_1 , ..., y_n) = \prod^{n}_{i=1}f(y_i)\\\\
実際に求める時は、計算しやすくするため、\\\\
対数変換をした下記を用いてβを求めます。\\\\
logf(y_1 , ..., y_n) = \sum^{n}_{i=1}logf(y_i)最後に
今回は線形回帰モデルの概要を説明しました。
線形回帰モデルは、説明変数の線型結合と対応付ける形なので、
比較的シンプルなモデルだと思います。
ですが、推定パラメータ(β)やモデル精度の良し悪しを判断するための様々な検定や指標があり、”説明力がある“という意味で実務で大変活用できるモデルです。