「正規Q-Qプロット」の概要
一言で言うと「データが正規分布か?」を調べる手法です。
少し詳細にすると、「データと標準正規分布の “分位点を比較できるようにした” グラフ」(下図が一例)であり、「プロットした点が “直線に近ければ” 、対象データは正規分布に近いだろう」と考えます。
※「Q-Q」の「Q」は「quantile」(分位点)を指します。
「分位点」等、前提知識も軽く触れた上で、正規Q-Qプロットの説明をします。
前提知識
標準正規分布
一言で言うと、「平均 0 , 分散 1 の正規分布」です。
正規分布については以下の記事にまとめています。
分位点
厳密な用語定義は、他を参照いただくとして、ここでは、(後続の話を理解いただく上で必要な) ざっくりな説明をします。
まず、「データ値をソートし、”小さい値から順に、その確率を足し合わせる“こと」をイメージしてください。
その時に、「特定の確率値に至った時のデータ値」が分位点です。
例えば、標準正規分布のデータの場合、確率50%の分位点は 「0」です。
(“値が「0」以下”の確率が50%になるからです。)
正規分布 N(μ , σ^2) と 標準正規分布 N(0 , 1) の関係
先に伝えたいポイントを話すと、「(下記の関係があるため、)データが正規分布に従う時、理論上、正規Q-Qプロットは直線になる。」となります。
データxが正規分布に従う場合、平均μと分散σ^2が何であれ、下記の計算結果が標準正規分布になります。
\frac{x-μ}{σ} 〜 N(0 , 1)=Z \\\\
→どんな正規分布(x)でも、上記計算で標準正規分布(Z)になる。そのため、分位点を考えると、(任意の)正規分布と標準正規分布には下記の関係があります。
※下記x,yは、後続の説明に合わせて表記しています。
任意の確率αに対する分位点を考える。\\\\
標準正規分布と正規分布N(μ , σ^2)それぞれの分位点をx , yとすると、 \\\\
下記の関係式が成り立つ。\\\\
\\\\
x=\frac{y-μ}{σ}\\\\
\\\\
これは、"yはxの一次式(xはyの一次式)で表現される"形なので、\\\\
(x,y)は"直線上にプロット"される。これが、「正規Q-Qプロットで”プロットが直線になれば対象データは正規分布だろう”と判断できる理由」です。
「正規Q-Qプロット」の詳細
「正規Q-Qプロット」は、「標準正規分布と取得データの分位点n個をそれぞれ x_i , y_i (i=1,…n)と置き、xy平面上に、( x_i , y_i )をプロットする」ものです。
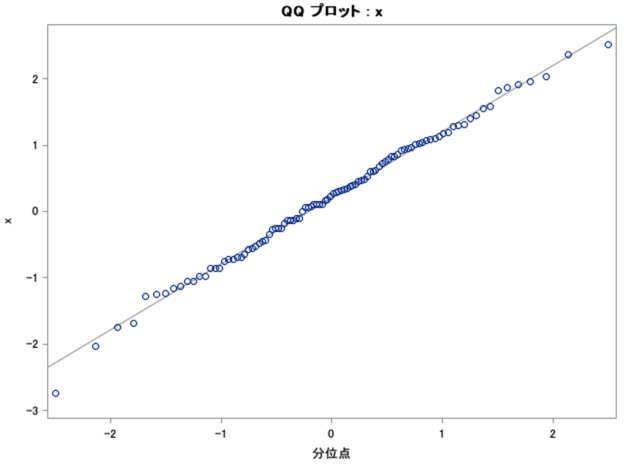
下図は、(SASで作成した) “正規分布のデータ“の正規Q-Qプロットです。
※複数ある○がプロットです。SASでは参考として直線も表示してくれます。
直線とプロット(○)を比較いただくと、”プロットが(大体)直線上にある“のが分かります。
データが正規分布であれば、下図の通り直線上にプロットされるので、「”直線上にプロットされてれば、データは正規分布だろう“」と考えます。
※直線になるのは、あくまで”正規分布の必要条件“なので、直線上にプロットされても、必ずしも正規分布とは限らない事に注意です。

最後に
正規Q-Qプロットの他にも正規性を調べる手法があります。
統計学では、”データが正規分布である“ことを前提とする手法が多く存在します。
正規Q-Qプロット含め正規性の調査は、上記前提の妥当性を調べる手法であるため、特に統計を実際に活用する上で重要なものだと筆者は考えています。