初めに
本記事は検定初学者向けに、”検定を実際にやって結果をどう見るか“について説明します。
SASでは、簡単なコードで様々な情報(集計結果)が出力されますが、今回は、”帰無仮説の棄却するか否かの判断“にポイントを絞って説明します。
また、本記事の説明では、”「1群の検定」(下記リンク)の概要を把握してる“前提で説明をします。
まだ把握されていない方は先に以下の記事をお読みください。
「2群の検定」、「対応の無い」とは
概要
簡単に言うと、「2グループの母平均・母分散が等しいか?」を調べる検定です。
1群の検定では特定値との比較をする形でしたが、2群の場合は両方のパラメータ値を比較する形になります。
また、タイトルにある「対応の無い」という意味について説明します。
2群の検定では、「対応のあり」と「対応の無い2群」の2ケースを区別しており、それぞれに対して検定が存在します。
今回説明する「対応の無い2群」は、統計学的には「“独立な確率分布にそれぞれに従う”2群」の検定であり、イメージとしては“各群には別々の人が存在する”ケースの話になります。
それに対して、「対応のある2群」は、統計学的には「“独立でない確率分布にそれぞれに従う”2群」の検定であり、イメージとしては“同じ人の治療前と治療後の結果を群として分ける”ケースの話になります。
帰無仮説 / 対立仮説
2群の検定対象としては、母平均と母分散があります。
それぞれ下記の通りに仮説を立てます。
母平均の検定
仮説は下記の通りに立てます。
但し、実際の集計方法は、仮定「母分散が等しいか不明か」によって変えます。
SASでは、(下記コードで)両ケースの集計が簡単に実行できます。
“どちらのケースが妥当か“の判断の際は、下記の「母分散の検定」の結果が判断材料になります。
帰無仮説 H_0 : μ_A = μ_B \\\\ 対立仮説 H_1 : μ_A ≠ μ_B \\\\ ※ μ_A(μ_B) : グループA(B)の母平均
母分散の検定
帰無仮説 H_0 : σ^2_A = σ^2_B \\\\ 対立仮説 H_1 : σ^2_A ≠ σ^2_B \\\\ ※ σ^2_A(σ^2_B) : グループA(B)の母分散
[SAS]データ作成 / 検定実施
それではデータ作成も含め、実際に検定のコードを書いてみましょう。
実施概要
下記フローでコードを書きます。
- テストデータ作成
- A群のデータ1,000件を作成 (標準正規分布)
- B群のデータ1,500件を作成 (標準正規分布)
- 上記1-1,1-2のデータを縦結合 (1つのデータセットにまとめる)
- 検定実施 (母平均・母分散の検定)
検定結果の想定
上記フローの 2. (検定実施) は、結果について想定ができます。
まず前提ですが、フローの 1. より、両グループのデータは標準正規分布、つまり “母平均 = 0 で 母分散 = 1 の分布“に従うように作成します。
なので、フローの 2. では、「仮定・実データ共に帰無仮説の通りであるため、集計結果が”(所謂)稀にはならず“、帰無仮説は棄却されない」という想定ができます。
検定結果を見るための予備知識
検定結果を読み取るために下記用語を説明します。
- 「F値」:(F分布に従う形に)データを集計した時の値。”これが、F分布の中で稀な位置付け(=値が大きい)になってるか”を確認する。(今回、等分散の検定にてF値を算出します。)
上記の他に「t値」や「P値」と言う用語が出てきますが、それらについては以下の記事をご確認ください。
SASコード
上記を踏まえて、実際にコードを書いてみましょう。
/* 1-1. [Aグループ]標準正規分布のデータ作成(2,000レコード) */
data data_a(drop=i);
group = 'A';
do i=1 to 1000;
x = rand('NORMAL');
output;
end;
run;
/* 1-2. [Bグループ]標準正規分布のデータ作成(2,000レコード) */
data data_b(drop=i);
group = 'B';
do i=1 to 1500;
x = rand('NORMAL');
output;
end;
run;
/* 1-3. [A & Bグループ]データを縦結合(1つのデータセットにまとめる) */
data data_all;
set data_a data_b;
run;
/* 2. 対応無し2群の検定 */
/* ① 等分散性の検定:帰無仮説:両群の母分散が等しい ※想定:帰無仮説は棄却されない */
/* ② 母平均の検定:帰無仮説:両群の母平均が等しい ※想定:帰無仮説は棄却されない */
proc ttest data=data_all;
class group;
var x;
run;[実行結果] 作成データ
下記のようなデータ(data_all)が作成できます。
両群 (group=’A’ , ‘B’共に) 標準正規分布に従うようにデータを作成したため、大体のデータが0に近くなっています。
| group | x |
|---|---|
| A | 0.39030 |
| A | 1.14290 |
| … | … |
| B | -0.18346 |
| B | 0.07581 |
[実行結果] 検定結果 (母平均・母分散の検定)
検定の結果として、数表と図が表示されます。
“帰無仮説の棄却するか否かの判断“においては数表を確認します。
数表は以下のようになりました。
各検定結果ですが、(結論としては)下記箇所を確認します。
- 母分散の検定:下表
- 母平均の検定:上表の[手法]=「Pooled」※理由は下記で説明。
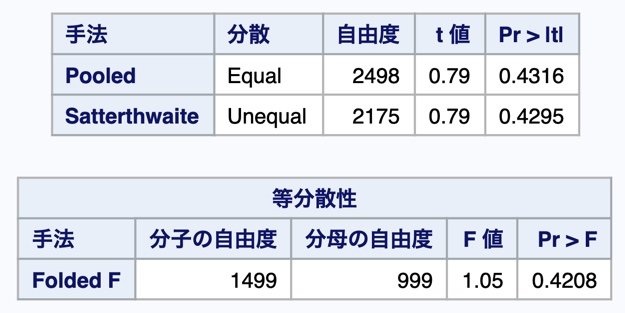
母分散の検定結果
「Pr > |t|」はP値を指し、今回”P値は約42.08%“になりました。
一般に有意水準 (帰無仮説を棄却するP値基準) は10%や5%であり、それらと比較し、今回のP値は遥かに大きいです。
なので、”帰無仮説を仮定すると取得データはそんなに稀な値ではない“という形のため、帰無仮説は棄却されません。
母平均の検定結果
今回は、[手法]=「Pooled」(※1)を確認します。
理由としては下記2点です。
- 上記[母分散の検定結果]より、「”母分散が等くない”とは言えない」という結果のため
- 母分散が同じだろうと想定してる(という体)のため
確認方法ですが、(母分散と同様に)「Pr > |t|」(P値)を確認します。
今回”P値は約43.16%“になり、これは、一般の有意水準 (10%,5%)と比べ、遥かに大きいです。
なので、”帰無仮説を仮定すると取得データはそんなに稀な値ではない“という形のため、帰無仮説は棄却されません。
(※1)各結果(手法)の内容は下記の通りです。つまり、“母分散の仮定”が異なり、その仮定に合った集計の結果が出力されています。
- Pooled:”母分散が等しい“と仮定した時のt値/P値 (利用する分散推定量が「pooled variance」)
- Satterthwaite:”母分散が等しいか不明である“と仮定した時のt値/P値 (t値とする集計結果が「Satterthwaite の近似」)
最後に
今回の検定では(t値に加え、)等分散性の検定にてF値が出ました。
F分布については下記をご参照ください。