初めに
正規分布は、統計学を学び始めた方が(恐らく)最初に学ぶであろう分布です。
本記事では、理論を学び始めた方をターゲットに、”詳細の説明はせず、概要として押さえておきたい”ポイントをまとめていきます。
「正規分布」とは
ざっくり言うと、「平均値を軸に左右対称の釣鐘状の分布」です。
下図のようなグラフになります。(平均値は100)
パッと見ての通り、平均が一番確率が高く、平均から離れる程、(左右対称に)確率が低くなる分布です。

ちなみに確率を数式で表すと下記の通りです。
※ x が データ値(上図における横軸) 、f(x) が確率(上図における縦軸)です。
[正規分布] ※平均 = μ , 分散 = σ^2
\\\\
\\\\
f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{-\frac{(x-\mu)^2}{2\sigma^2}}複雑な数式に見えるかもしれません。
(統計学の概要だけ学ぶなら別ですが、)正規分布は統計学の様々な話で関わる分布のため、(少なくとも)「こんな感じの数式だったな」程度でも把握しておく必要があります。
(詳細の話をすると、下記数式の構成は ガウス積分 × 係数(帳尻合わせ)と言う形であり、係数は”全区間で積分すると1になる“ように設定されています。)
「正規分布」の特徴
ターゲットは上記で記載した通りのため、詳細な話はせず、ポイントを絞って説明します。
平均と分散で一意に決まる
正規分布は、左右対称の釣鐘状であることは決まっていますが、上図のように、「平均が100で裾野がこの形」と固定された分布名ではありません。
平均と分散をパラメータとして設けている分布であり、(データ等に合わせて、)平均や分散を決めることで一意の形状になります。
データ量が膨大の時、その平均は”どんなデータでも“正規分布に近似される
※数学的に、厳密に話すと語弊が出てきますが、”ざっくりのイメージとしては“表題の通りです。
「ちょっと何を言ってるか分からない」かも知れません。
下記をイメージしてみてください。
- 特定の観測データをたくさん取得。
- 取得したデータから平均を算出。(総和をデータ数で割る。)
“その算出した平均の分布がどうなっているか?“という話です。
少し数学的に話すと、「データ量が限りなく多い時、算出した平均は限りなく正規分布に近づく。」です。
この性質は、データが”どんな分布でも“成り立つ話であり、筆者的に”「正規分布が凄い」と思う一番の理由”です。
※この性質は「中心極限定理」という定理で示されています。深掘りたい方は調べてみてください。
68–95–99.7則
こちらは、端的に言うと、”標準偏差σから定められた区間の確率“です。
※標準偏差σは、パラメータの一つである分散の(正の)平方根です。
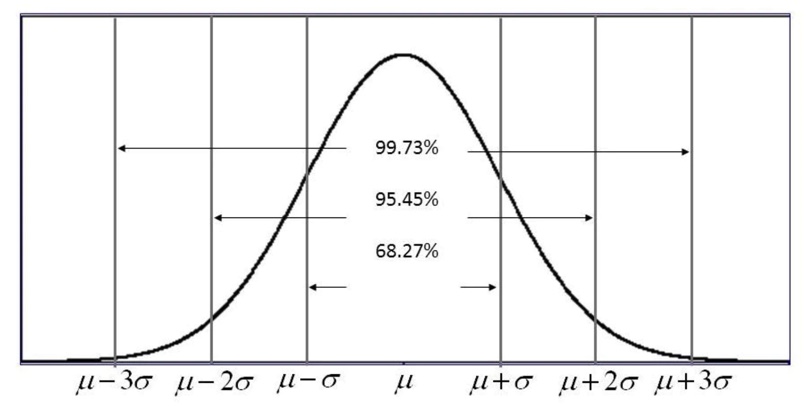
具体的には、”平均μを中心とした時に、-σ 〜 σ、-2σ 〜 2σ、-3σ 〜 3σそれぞれの区間の確率“になります。
図にすると下図の通りであり、”偏差値から、自分が上位何%なのかざっくり把握する“等で利用されたり、正規分布を活用するにあたって、初歩として押さえておいた方が良いと思います。
最後に
統計理論を学び始めた方をターゲットに、ポイントを絞って正規分布の特徴を説明しました。
正規分布は、(一般にもよく仮定される分布なので) 実用性があり、且つ、統計学において様々な話や分布と関わるので、是非深掘ってみてください。